题目内容
在等边三角形ABC中,∠B和∠C的角平分线相交于点O,则∠BOC等于
- A.100°
- B.110°
- C.120°
- D.130°
C
分析:根据题意画出图形,再结合等边三角形三线合一的性质及三角形内角和定理进行解答即可.
解答: 解:如图所示:
解:如图所示:
∵△ABC是等边三角形,BD、CE分别是∠ABC与∠ACB的平分线,
∴∠DBC= ∠ABC=
∠ABC= ×60°=30°,∠BCE=
×60°=30°,∠BCE= ∠ACB=
∠ACB= ×60°=30°,
×60°=30°,
∴∠DBC=∠BCE=30°,
∴∠BOC=180°-∠DBC-∠BCE=180°-30°-30°=120°.
故选C.
点评:本题考查的是等边三角形的性质,解答此类题目时往往用到三角形的内角和是180°这一隐含条件.
分析:根据题意画出图形,再结合等边三角形三线合一的性质及三角形内角和定理进行解答即可.
解答:
 解:如图所示:
解:如图所示:∵△ABC是等边三角形,BD、CE分别是∠ABC与∠ACB的平分线,
∴∠DBC=
 ∠ABC=
∠ABC= ×60°=30°,∠BCE=
×60°=30°,∠BCE= ∠ACB=
∠ACB= ×60°=30°,
×60°=30°,∴∠DBC=∠BCE=30°,
∴∠BOC=180°-∠DBC-∠BCE=180°-30°-30°=120°.
故选C.
点评:本题考查的是等边三角形的性质,解答此类题目时往往用到三角形的内角和是180°这一隐含条件.

练习册系列答案
相关题目
 20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理. 17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.
17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.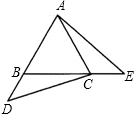 已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE.
已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE. 如图,在等边三角形ABC中,D为AC的中点,
如图,在等边三角形ABC中,D为AC的中点,