题目内容
 如图,AB⊥BC,AB=BC=2cm,
如图,AB⊥BC,AB=BC=2cm, 与
与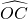 关于点O中心对称,则AB、BC、
关于点O中心对称,则AB、BC、 、
、 所围成的图形的面积是________cm2.
所围成的图形的面积是________cm2.
2
分析:连AC,则△ABC为等腰直角三角形,由 与
与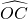 关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、
关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、 、
、 所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.
所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.
解答:连AC,如图 ,
,
∵AB⊥BC,AB=BC=2cm,
∴△ABC为等腰直角三角形,
又∵ 与
与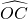 关于点O中心对称,
关于点O中心对称,
∴OA=OC,弧OA=弧OC,
∴弓形OA的面积=弓形OC的面积,
∴AB、BC、 、
、 所围成的图形的面积=三角形ABC的面积=
所围成的图形的面积=三角形ABC的面积= ×2×2=2(cm2).
×2×2=2(cm2).
故答案为2.
点评:本题考查了等腰直角三角形的性质:等腰直角三角形的两腰相等,两锐角都为45°;也考查了中心对称的性质以及三角形的面积公式.
分析:连AC,则△ABC为等腰直角三角形,由
 与
与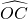 关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、
关于点O中心对称得到OA=OC,弧OA=弧OC,则弓形OA的面积=弓形OC的面积,因此AB、BC、 、
、 所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.
所围成的图形的面积=三角形ABC的面积,然后根据直角三角形的面积公式计算即可.解答:连AC,如图
 ,
,∵AB⊥BC,AB=BC=2cm,
∴△ABC为等腰直角三角形,
又∵
 与
与 关于点O中心对称,
关于点O中心对称,∴OA=OC,弧OA=弧OC,
∴弓形OA的面积=弓形OC的面积,
∴AB、BC、
 、
、 所围成的图形的面积=三角形ABC的面积=
所围成的图形的面积=三角形ABC的面积= ×2×2=2(cm2).
×2×2=2(cm2).故答案为2.
点评:本题考查了等腰直角三角形的性质:等腰直角三角形的两腰相等,两锐角都为45°;也考查了中心对称的性质以及三角形的面积公式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S= 12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
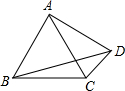 如图,AB=BC=AC=AD,那么∠BDC等于( )
如图,AB=BC=AC=AD,那么∠BDC等于( ) 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为