题目内容
如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，∠1=∠2．
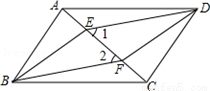
（1）求证：AE=CF；
（2）求证：四边形EBFD是平行四边形．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
海淀黄冈名师导航系列答案普通高中同步练习册系列答案优翼小帮手同步口算系列答案题目内容
如图，四边形ABCD是平行四边形，E、F是对角线AC上的两点，∠1=∠2．
（1）求证：AE=CF；
（2）求证：四边形EBFD是平行四边形．
海淀黄冈名师导航系列答案普通高中同步练习册系列答案优翼小帮手同步口算系列答案
(k≠0)的图像经过点B、D时，k=______．
B. 10－4÷10－2=0．01 C. 
2n÷
；（2）
.
，xy=
，则代数式（x-1）（y+1）的值等于___________。