题目内容
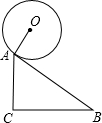 如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?
如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?
分析:作⊙O的直径EF,使EF∥AC,AD⊥OF,则油桶最高点的高度为AC+DE;如图,可知AD∥BC,∠B=∠DAB,∠B+∠BAC=∠DAB+∠OAD=90°,所以,△ABC∽△AOD,
=
,代入即可得出OD的长,即可解答出;
| OA |
| AB |
| OD |
| BC |
解答: 解:∵直角△ABC中,AB=5,AC=3,∴BC=4,
解:∵直角△ABC中,AB=5,AC=3,∴BC=4,
作⊙O的直径EF,使EF∥AC,AD⊥OF,如图,
∴AD∥BC,
∵油桶与斜面相切于A处,
∴∠B=∠DAB,∠B+∠BAC=∠DAB+∠OAD=90°,
即∠BAC=∠OAD,
∴△ABC∽△AOD,
∴
=
,
∴
=
,
即OD=0.8;
∴油桶最高点的高度=AC+OD+OE=3+0.8+1=4.8(米).
答:油桶最高点的高度为4.8米.
 解:∵直角△ABC中,AB=5,AC=3,∴BC=4,
解:∵直角△ABC中,AB=5,AC=3,∴BC=4,作⊙O的直径EF,使EF∥AC,AD⊥OF,如图,
∴AD∥BC,
∵油桶与斜面相切于A处,
∴∠B=∠DAB,∠B+∠BAC=∠DAB+∠OAD=90°,
即∠BAC=∠OAD,
∴△ABC∽△AOD,
∴
| OA |
| AB |
| OD |
| BC |
∴
| 1 |
| 5 |
| OD |
| 4 |
即OD=0.8;
∴油桶最高点的高度=AC+OD+OE=3+0.8+1=4.8(米).
答:油桶最高点的高度为4.8米.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目


 如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?
如图为斜面和圆柱形油桶的截面图,斜面AB=5,A点垂直高度AC=3米,油桶的半径为1米,当油桶与斜面相切于A处时,求油桶最高点的高度?