题目内容
如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于
- A.90°
- B.135°
- C.150°
- D.270°
D
分析：由四边形内角和公式可求∠1+∠2+∠A+∠B=360°，又在Rt△ABC中，∠C=90°，可知∠A+∠B=90°，由此求∠1+∠2．
解答：∵ABED为四边形，
∴∠1+∠2+∠A+∠B=360°，
又∵在Rt△ABC中，∠C=90°，
∴∠A+∠B=90°，
∴∠1+∠2=360°-（∠A+∠B）=270°．
故选D．
点评：本题考查了多边形外角与内角．此题比较简单，关键是利用三角形的内角和，四边形的内角和求解．
分析：由四边形内角和公式可求∠1+∠2+∠A+∠B=360°，又在Rt△ABC中，∠C=90°，可知∠A+∠B=90°，由此求∠1+∠2．
解答：∵ABED为四边形，
∴∠1+∠2+∠A+∠B=360°，
又∵在Rt△ABC中，∠C=90°，
∴∠A+∠B=90°，
∴∠1+∠2=360°-（∠A+∠B）=270°．
故选D．
点评：本题考查了多边形外角与内角．此题比较简单，关键是利用三角形的内角和，四边形的内角和求解．
练习册系列答案
相关题目
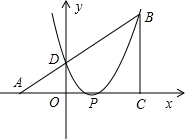，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．
如图，已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．
25、如图，已知△ABC为等边三角形，D、F分别为BC、AB边上的点，CD=BF，以AD为边作等边△ADE．
如图，已知△ABC为等边三角形，D，E，F分别在边BC，CA，AB上，且△DEF也是等边三角形，除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的．
如图，已知△ABC为等边三角形，点D．E分别在BC．AC边上，且AE=CD，AD与BE相交于点F．