题目内容
【题目】某水果店每天的房租、人员工资等固定成本250元，水果进价是5元/斤，物价局规定售价不得高于12元/斤，也不得低于7元/斤，调查发现日均销量y（斤）与售价x（元）满足一次函数关系，图象如图．
（1）求日均销量y（斤）与销售单价x（元）之间的函数关系式，并写出自变量取值范围；
（2）设每天净利润为W元，那么定价多少时，可获得最大净利润？最大是多少？
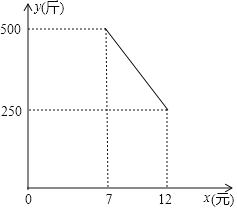
【答案】（1）y＝﹣50x+850（7≤x≤12）；（2）当定价为11元时，可获得最大利润，最大是1550元．
【解析】
（1）根据待定系数法，可得一次函数解析式；
（2）根据每桶利润乘以数量，可得总利润．
解：（1）设y与x之间的函数关系式为y＝kx+b，
则7k+b=500 12k+b=250
解得k=-50 b=850
∴y＝﹣50x+850（7≤x≤12）；
（2）由题意得w＝（x﹣5）y﹣250＝（x﹣5）（﹣50x+850）﹣250
＝﹣50（x﹣5）（x﹣17）﹣250
＝﹣50（x2﹣22x+85）﹣250
＝﹣50（x2﹣22x+121﹣121+85）﹣250
＝﹣50（x﹣11）2+50×36﹣250
＝﹣50（x﹣11）2+1550，
∵﹣50＜0，对称轴直线x＝11，7≤x≤12
∴当x＝11时，Wmax＝1550元，
答：当定价为11元时，可获得最大利润，最大是1550元．
【题目】如图，在平行四边形ABCD中，∠ABC＝45°，AB＝4
，BC＝9，直线MN平分平行四边形ABCD的面积，分别交边AD、BC于点M、N，若△BMN是以MN为腰的等腰三角形，则BN＝_____．
【题目】太阳山中学九年级举行跳绳比赛，要求每班选出
名学生参加，在规定时间内每人跳绳不低于
次为优秀，冠、亚军会在甲、乙两班中产生，下表是这两个班的5名学生的比赛数据(单位:次)
|
|
|
|
| 平均次数 | 方差 | |
甲班 |
|
|
|
|
|
|
|
乙班 |
|
|
|
|
|
|
|
根据以上信息，解答下列问题:
（1）求出表中
的值和甲、乙两班比赛学生的优秀率;
（2）求出两班的跳绳比赛数据的中位数;
（3）请你结合表格和自己所算出的数据判断冠军应发给哪个班?简要说明理由.
