题目内容
 将0,1,2,3,4,5,6,7,8,9分别填入图中的十个圆圈内(每个数只填一次),使得各个阴影三角形的三个顶点处的圆圈内所填数之和都相等.则A处的圆圈内所有可以填入的数是________.
将0,1,2,3,4,5,6,7,8,9分别填入图中的十个圆圈内(每个数只填一次),使得各个阴影三角形的三个顶点处的圆圈内所填数之和都相等.则A处的圆圈内所有可以填入的数是________.
3或6
分析:由于每个阴影三角形的三个顶点处的圆圈内的数之和相等,而图中有6个阴影三角形,所以6个三角形18个顶点处的数之和应是6的倍数,最中间的一个数出现3次,最外面的3个数出现1次,其余的6个数都出现2次.
解答:本题有两种三角形:

一、每顶点上的一个圆圈和顶点的每一边的一个圆圈组成的三角形,共三个;
二、中间的一个圆圈和一边上的两个圆圈组成的三角形,共三个;顶点上的三个三角形的9个圆圈和中间的1个圆圈用的10个数字是不重复的,顶点上的三个三角形,要求每个三角形的三个圆圈的和相等,所以,顶点上的三个三角形的9个圆圈的和能被3整除,因为45能被3整除,所以,中间可能填的数为0、3、6、9,四个数中的一个;
①中间填0,顶点上的三个三角形,每个三角形的和是 =15,中间的数和每边上的两个数和要为15,每边上的两个数和为15-0=15,在1-9中,只有7+8=15、6+9=15,两组等于15的数字,所以中间不能填0;
=15,中间的数和每边上的两个数和要为15,每边上的两个数和为15-0=15,在1-9中,只有7+8=15、6+9=15,两组等于15的数字,所以中间不能填0;
②中间填3,顶点上的三个三角形,每个三角形的和是 =14,中间的数和每边上的两个数和要为14,每边上的两个数和为14-3=11,在0-2、3-9中,有5+6=11、4+7=11、2+9=11,三组等于11的数字,所以中间可以填3;顶点上的三个三角形填的数字为,0+5+9=14、1+6+7=14、8+2+4=14;填3可以;
=14,中间的数和每边上的两个数和要为14,每边上的两个数和为14-3=11,在0-2、3-9中,有5+6=11、4+7=11、2+9=11,三组等于11的数字,所以中间可以填3;顶点上的三个三角形填的数字为,0+5+9=14、1+6+7=14、8+2+4=14;填3可以;
③中间填6,顶点上的三个三角形,每个三角形的和是 =13,中间的数和每边上的两个数和要为13,每边上的两个数和为13-6=7,在0-5、7-9中,有3+4=7、2+5=7、0+7=7,三组等于7的数字,所以中间可以填6;顶点上的三个三角形填的数字为,1+5+7=13、8+2+3=13、9+0+4=13;填6可以;
=13,中间的数和每边上的两个数和要为13,每边上的两个数和为13-6=7,在0-5、7-9中,有3+4=7、2+5=7、0+7=7,三组等于7的数字,所以中间可以填6;顶点上的三个三角形填的数字为,1+5+7=13、8+2+3=13、9+0+4=13;填6可以;
④中间填9,顶点上的三个三角形,每个三角形的和是 =12,中间的数和每边上的两个数和要为12,每边上的两个数和为12-9=3,在0-8中,只有1+2=3、0+3=3,两组等于3的数字,所以中间不能填9;
=12,中间的数和每边上的两个数和要为12,每边上的两个数和为12-9=3,在0-8中,只有1+2=3、0+3=3,两组等于3的数字,所以中间不能填9;
故答案为:3或6.
点评:此题主要考查了数字的规律,注意观察数据之间的规律,得出三角形顶点和的规律,比较新颖.
分析:由于每个阴影三角形的三个顶点处的圆圈内的数之和相等,而图中有6个阴影三角形,所以6个三角形18个顶点处的数之和应是6的倍数,最中间的一个数出现3次,最外面的3个数出现1次,其余的6个数都出现2次.
解答:本题有两种三角形:

一、每顶点上的一个圆圈和顶点的每一边的一个圆圈组成的三角形,共三个;
二、中间的一个圆圈和一边上的两个圆圈组成的三角形,共三个;顶点上的三个三角形的9个圆圈和中间的1个圆圈用的10个数字是不重复的,顶点上的三个三角形,要求每个三角形的三个圆圈的和相等,所以,顶点上的三个三角形的9个圆圈的和能被3整除,因为45能被3整除,所以,中间可能填的数为0、3、6、9,四个数中的一个;
①中间填0,顶点上的三个三角形,每个三角形的和是
 =15,中间的数和每边上的两个数和要为15,每边上的两个数和为15-0=15,在1-9中,只有7+8=15、6+9=15,两组等于15的数字,所以中间不能填0;
=15,中间的数和每边上的两个数和要为15,每边上的两个数和为15-0=15,在1-9中,只有7+8=15、6+9=15,两组等于15的数字,所以中间不能填0;②中间填3,顶点上的三个三角形,每个三角形的和是
 =14,中间的数和每边上的两个数和要为14,每边上的两个数和为14-3=11,在0-2、3-9中,有5+6=11、4+7=11、2+9=11,三组等于11的数字,所以中间可以填3;顶点上的三个三角形填的数字为,0+5+9=14、1+6+7=14、8+2+4=14;填3可以;
=14,中间的数和每边上的两个数和要为14,每边上的两个数和为14-3=11,在0-2、3-9中,有5+6=11、4+7=11、2+9=11,三组等于11的数字,所以中间可以填3;顶点上的三个三角形填的数字为,0+5+9=14、1+6+7=14、8+2+4=14;填3可以;③中间填6,顶点上的三个三角形,每个三角形的和是
 =13,中间的数和每边上的两个数和要为13,每边上的两个数和为13-6=7,在0-5、7-9中,有3+4=7、2+5=7、0+7=7,三组等于7的数字,所以中间可以填6;顶点上的三个三角形填的数字为,1+5+7=13、8+2+3=13、9+0+4=13;填6可以;
=13,中间的数和每边上的两个数和要为13,每边上的两个数和为13-6=7,在0-5、7-9中,有3+4=7、2+5=7、0+7=7,三组等于7的数字,所以中间可以填6;顶点上的三个三角形填的数字为,1+5+7=13、8+2+3=13、9+0+4=13;填6可以;④中间填9,顶点上的三个三角形,每个三角形的和是
 =12,中间的数和每边上的两个数和要为12,每边上的两个数和为12-9=3,在0-8中,只有1+2=3、0+3=3,两组等于3的数字,所以中间不能填9;
=12,中间的数和每边上的两个数和要为12,每边上的两个数和为12-9=3,在0-8中,只有1+2=3、0+3=3,两组等于3的数字,所以中间不能填9;故答案为:3或6.
点评:此题主要考查了数字的规律,注意观察数据之间的规律,得出三角形顶点和的规律,比较新颖.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
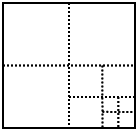 将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:
将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:| 操作次数 | 1 | 2 | 3 | 4 | … |
| 所得正方形的总个数 | 4 | 7 | 10 | 13 | … |
(2)从表格和第(1)题的结果中你发现了什么?我发现
(3)请你根据你的发现归纳出:当操作次数为n次时,得到的正方形的个数是
(4)仔细观察图形,请你利用图形揭示的规律进行下面的计算(要有揭示规律的过程):
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
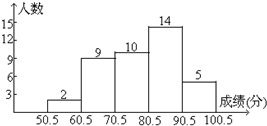 高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题: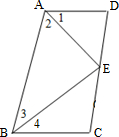 22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.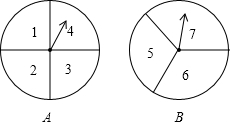 小亮获胜.
小亮获胜.