题目内容
 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为
如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为
- A.

- B.
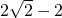
- C.

- D.

A
分析:如图,延长CB至L,使BL=DN,则Rt△ABL≌Rt△AND,故AL=AN,进而求证△AMN≌△AML,即可求得∠MAN=∠MAL=45°设CM=x,CN=y,MN=z,根据x2+y2=z2,和x+y+z=2,整理根据△=4(z-2)2-32(1-z)≥0可以解题.
解答:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△AND,
故AL=AN,
∴△AMN≌△AML,
∴∠MAN=∠MAL=45°,
设CM=x,CN=y,MN=z
x2+y2=z2,
∵x+y+z=2,
则x=2-y-z
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
∴△=4(z-2)2-32(1-z)≥0,
即(z+2+2 )(z+2-2
)(z+2-2 )≥0,
)≥0,
又∵z>0,
∴z≥2 -2,当且仅当x=y=2-
-2,当且仅当x=y=2- 时等号成立
时等号成立
此时S△AMN=S△AML= ML•AB=
ML•AB= z
z
因此,当z=2 -2,x=y=2-
-2,x=y=2- 时,S△AMN取到最小值为
时,S△AMN取到最小值为  -1.
-1.
故选A.
点评:本题考查了勾股定理在直角三角形中的运用,考查了正方形各边长相等,各内角为直角的性质,本题中求证△AMN≌△AML是解题的关键.
分析:如图,延长CB至L,使BL=DN,则Rt△ABL≌Rt△AND,故AL=AN,进而求证△AMN≌△AML,即可求得∠MAN=∠MAL=45°设CM=x,CN=y,MN=z,根据x2+y2=z2,和x+y+z=2,整理根据△=4(z-2)2-32(1-z)≥0可以解题.
解答:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△AND,

故AL=AN,
∴△AMN≌△AML,
∴∠MAN=∠MAL=45°,
设CM=x,CN=y,MN=z
x2+y2=z2,
∵x+y+z=2,
则x=2-y-z
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
∴△=4(z-2)2-32(1-z)≥0,
即(z+2+2
 )(z+2-2
)(z+2-2 )≥0,
)≥0,又∵z>0,
∴z≥2
 -2,当且仅当x=y=2-
-2,当且仅当x=y=2- 时等号成立
时等号成立此时S△AMN=S△AML=
 ML•AB=
ML•AB= z
z因此,当z=2
 -2,x=y=2-
-2,x=y=2- 时,S△AMN取到最小值为
时,S△AMN取到最小值为  -1.
-1.故选A.
点评:本题考查了勾股定理在直角三角形中的运用,考查了正方形各边长相等,各内角为直角的性质,本题中求证△AMN≌△AML是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )
如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( ) B、
B、 C、
C、 D、
D、







 B、
B、 C、
C、 D、
D、
