题目内容
【题目】已知,ABCD中,∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

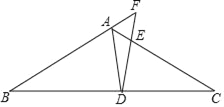
(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
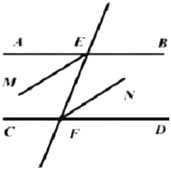
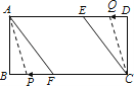
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
【答案】(1)证明见解析;(2)AF=5;(3)以A,C,P,Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.
【解析】
(1)先证明四边形![]() 为平行四边形,再根据对角线互相垂直平分的四边形是菱形作出判定;
为平行四边形,再根据对角线互相垂直平分的四边形是菱形作出判定;
(2)根据勾股定理即可求![]() 的长;
的长;
(3)分情况讨论可知,![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,![]() .
.
![]() 垂直平分
垂直平分![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
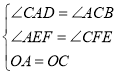 ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 四边形
四边形![]() 为菱形.
为菱形.
(2)设菱形的边长![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,由勾股定理,得
,由勾股定理,得
![]() ,
,
解得:![]() ,
,
![]() .
.
(3)由作图可以知道,![]() 点
点![]() 上时,
上时,![]() 点
点![]() 上,此时
上,此时![]() ,
,![]() ,
,![]() ,
,![]() 四点不可能构成平行四边形;
四点不可能构成平行四边形;
同理![]() 点
点![]() 上时,
上时,![]() 点
点![]() 或
或![]() 上,也不能构成平行四边形.
上,也不能构成平行四边形.
![]() 只有当
只有当![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上时,才能构成平行四边形,
上时,才能构成平行四边形,
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,
![]() ,
,
![]() 点
点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,
秒,
![]() ,
,![]() ,
,
![]() ,
,
解得:![]() .
.
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() 秒.
秒.

 阅读快车系列答案
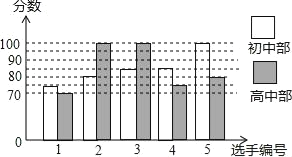
阅读快车系列答案【题目】某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 | 85 |
| 85 |
高中代表队 |
| 80 |
|
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.