题目内容
【题目】如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD. 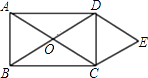
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为8 ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:∵DE∥OC,CE∥OD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴四边形OCED是菱形
(2)解:∵∠ACB=30°,
∴∠DCO=90°﹣30°=60°.
又∵OD=OC,
∴△OCD是等边三角形.
过D作DF⊥OC于F,则CF= ![]() OC,设CF=x,则OC=2x,AC=4x.
OC,设CF=x,则OC=2x,AC=4x.
在Rt△DFC中,tan60°= ![]() ,
,
∴DF= ![]() x.
x.
∴OCDF=8 ![]() .
.
∴x=2.
∴AC=4×2=8.
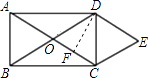
【解析】(1)熟记菱形的判定定理,本题可用一组邻边相等的平行四边形是菱形.(2)因为∠ACB=30°可证明菱形的一条对角线和边长相等,可证明和对角线构成等边三角形,然后作辅助线,根据菱形的面积已知可求解.
【考点精析】根据题目的已知条件,利用矩形的性质和解直角三角形的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.