题目内容
如图,在平面直角坐标系中,直线y=﹣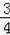
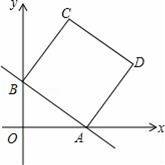
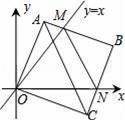
 x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.

【考点】一次函数综合题.
【分析】(1)把(4,0)代入y=﹣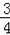
 x+b即可求得b的值;
x+b即可求得b的值;
(2)过点D作DE⊥x轴于点E,证明△OAB≌△EDA,即可求得AE和DE的长,则D的坐标即可求得;
(3)分当OM=MB=BN=NO时;当OB=BN=NM=MO=3时两种情况进行讨论.
【解答】解:(1)把(4,0)代入y=﹣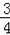
 x+b,得:﹣3+b=0,解得:b=3,
x+b,得:﹣3+b=0,解得:b=3,
故答案是:3;
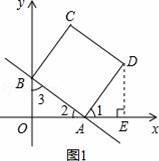
(2)如图1,过点D作DE⊥x轴于点E,
∵正方形ABCD中,∠BAD=90°,
∴∠1+∠2=90°,
又∵直角△OAB中,∠1+∠2=90°,
∴∠1=∠3,
在△OAB和△EDA中,
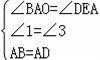
 ,
,
∴△OAB≌△EDA,
∴AE=OB=3,DE=OA=4,
∴OE=4+3=7,
∴点D的坐标为(7,4);
(3)存在.
①如图2,当OM=MB=BN=NO时,四边形OMBN为菱形.
则MN在OB的中垂线上,则M的纵坐标是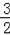
 ,
,
把y=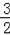
 代入y=﹣
代入y=﹣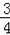
 x+4中,得x=2,即M的坐标是(2,
x+4中,得x=2,即M的坐标是(2,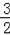
 ),
),
则点N的坐标为(﹣2,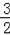
 ).
).
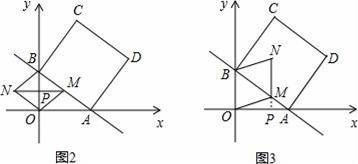

②如图3,当OB=BN=NM=MO=3时,四边形BOMN为菱形.
∵ON⊥BM,
∴ON的解析式是y=
 x.
x.
根据题意得: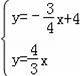
 ,
,
解得: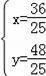
 .
.
则点N的坐标为(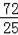
 ,
,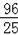
 ).
).


在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
 ( )
( ) D.三角形的高至少有一条在三角形内
D.三角形的高至少有一条在三角形内





 的图像大致为( )
的图像大致为( )