题目内容
 (2012•通辽)如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为
(2012•通辽)如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为30°
30°
.分析:由梯形ABCD中,AD∥BC,DC⊥BC,∠A′BC=15°,利用三角形外角的性质,可求得∠DA′B的度数,由折叠的性质,可得:∠A=∠DA′B=105°,∠ABD=∠A′BD,继而求得∠A′BD的度数.
解答:解:∵梯形ABCD中,AD∥BC,DC⊥BC,
∴∠C=90°,
∵∠A′BC=15°,
∴∠DA′B=∠A′BC+∠C=15°+90°=105°,
由折叠的性质可得:∠A=∠DA′B=105°,∠ABD=∠A′BD,
∵AD∥BC,
∴∠ABC=180°-∠A=75°,
∴∠A′BD=
=30°.
故答案为:30°.
∴∠C=90°,
∵∠A′BC=15°,
∴∠DA′B=∠A′BC+∠C=15°+90°=105°,
由折叠的性质可得:∠A=∠DA′B=105°,∠ABD=∠A′BD,
∵AD∥BC,
∴∠ABC=180°-∠A=75°,
∴∠A′BD=
| ∠ABC-∠A′BC |
| 2 |
故答案为:30°.
点评:此题考查了折叠的性质、梯形的性质以及三角形的外角的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
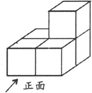 (2012•通辽)如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是( )
(2012•通辽)如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是( )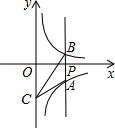 (2012•通辽)如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=-
(2012•通辽)如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=-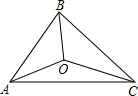 (2012•通辽)如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=
(2012•通辽)如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=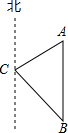 (2012•通辽)如图,小艳家(点A)在学校(点C)北偏东60°方向,AC=600(m).小颖家(点B)在小艳家正南,学校在小颖家北偏西45°方向.
(2012•通辽)如图,小艳家(点A)在学校(点C)北偏东60°方向,AC=600(m).小颖家(点B)在小艳家正南,学校在小颖家北偏西45°方向.