Question

【题目】对于一个函数给出如下定义：对于函数，若当，函数值满足，且满足，则称此函数为“属和合函数”．

例如：正比例函数，当时，，则，求得：，所以函数为“3属和合函数”．

（1）若一次函数为“1属和合函数”，则的值_________；

（2）已知二次函数，当时，是“属和合函数”，则的取值范围_________．

Answer 1

【答案】a＝1或a＝﹣1

【解析】

（1）分两种情况：利用“k属和合函数”的定义即可得出结论；

（2）分四种情况，各自确定出最大值和最小值，最后利用“k属和合函数”的定义即可得出结论；

解：（1）当a＞0时，
∵1≤x≤5，
∴a-1≤y≤5a-1，
∵函数y=ax-1（1≤x≤5）为“1属和合函数”，
∴（5a-1）-（a-1）=5-1，
∴a=1；
当a＜0时，（a-1）-（5a-1）=5-1，
∴a=-1，

∴a＝1或a＝-1；

（2）∵二次函数y=-3x2+6ax+a2+2a的对称轴为直线x=a，
∵当-1≤x≤1时，y是“k属和合函数”，
∴当x=-1时，y=a2-4a-3，
当x=1时，y=a2+8a-3，
当x=a时，y=4a2+2a，
①如图1，当a≤-1时，
当x=-1时，有ymax=a2-4a-3，
当x=1时，有ymin=a2+8a-3
∴（a2-4a-3）-（a2+8a-3）=2k，
∴k=-6a，
∴k≥6；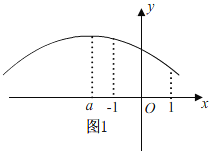

②如图2，当-1＜a≤0时，
当x=a时，有ymax=4a2+2a，
当x=1时，有ymin=a2+8a-3
∴（4a2+2a）-（a2+8a-3）=2k，
∴k=（a-1）2，
∴≤k＜6；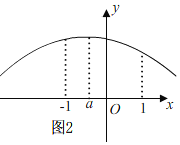

③如图3，当0＜a≤1时，
当x=a时，有ymax=4a2+2a，
当x=-1时，有ymin=a2-4a-3
∴（4a2+2a）-（a2-4a-3）=2k，
∴k=＜k≤6；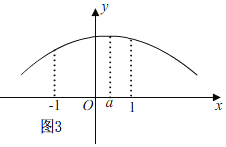

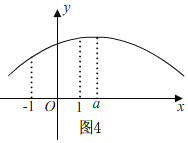
④如图4，当a＞1时，
当x=1时，有ymax=a2+8a-3，
当x=-1时，有ymin=a2-4a-3
∴（a2+8a-3）-（a2-4a-3）=2k，
∴k=-6a，
∴k＞6；

即：k的取值范围为k≥.