题目内容
 如图,已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B1处,DB1、EB1分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为
如图,已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B1处,DB1、EB1分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为
- A.45°
- B.50°
- C.55°
- D.60°
B
分析:由对顶角相等可得∠CHE=∠FHB1,由两角对应相等可得△ADM∽△B1HM,那么所求角等于∠ADM的度数.
解答: 解:由翻折可得∠B1=∠B=60°,
解:由翻折可得∠B1=∠B=60°,
∴∠A=∠B1=60°,
∵∠AMD=∠HMB1,
∴△ADM∽△B1HM,
∴∠ADM=∠B1HM,
∵∠CHE=∠MHB1,
∴∠CHE=∠ADM=50°.
故选B.
点评:本题考查了翻折变换问题;得到所求角与所给角的度数的关系是解决本题的关键.
分析:由对顶角相等可得∠CHE=∠FHB1,由两角对应相等可得△ADM∽△B1HM,那么所求角等于∠ADM的度数.
解答:
 解:由翻折可得∠B1=∠B=60°,
解:由翻折可得∠B1=∠B=60°,∴∠A=∠B1=60°,
∵∠AMD=∠HMB1,
∴△ADM∽△B1HM,
∴∠ADM=∠B1HM,
∵∠CHE=∠MHB1,
∴∠CHE=∠ADM=50°.
故选B.
点评:本题考查了翻折变换问题;得到所求角与所给角的度数的关系是解决本题的关键.

练习册系列答案
相关题目
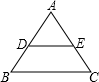
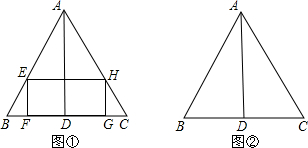
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动