题目内容
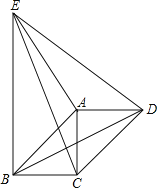
【题目】如图，在平面直角坐标系中，直线AB分别交x、y轴于点A、B，直线BC分别交x、y轴于点C、B，点A的坐标为（3，0），∠ABO=30°，且AB⊥BC．
（1）求直线BC和AB的解析式；
（2）将点B沿某条直线折叠到点O，折痕分别交BC、BA于点E、D，在x轴上是否存在点F，使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形？若存在，请求出F点坐标；若不存在，请说明理由；
（3）在平面直角坐标系内是否存在两个点，使得这两个点与B、C两点构成的四边形是正方形？若存在，请求出这两点的坐标；若不存在，请说明理由．
【答案】（1）y=
x+3
x，y=-x+3（2）点F（0，0）或（﹣3，0）（3）点M（﹣9﹣3，9），点N（﹣3，9+3）；点F（
，），点E坐标为（
，
）
【解析】
（1）根据题意可求点B，点C的坐标，用待定系数法可求解析式；（2）由题意可证DE是三角形的中位线，可求点D，点E的坐标，根据勾股定理可列方程，即可求点F的坐标；（3）分BC为边，BC为对角线讨论，根据正方形的性质，可求点的坐标．
（1）∵点A的坐标为（3，0）
∴AO=3
∵∠ABO=30°，∠AOB=90°
∴BO=AO=3，AB=2OA=6，∠OAB=60°，
又∵AB⊥BC
∴∠ACB=30°
∴AC=2AB=12
∴OC=AC﹣OA=12﹣3=9
∵OC=9，OB=3
∴点B（0，3），点C（﹣9，0）
设直线BC解析式y=kx+b
，
解得：k=，b=3
∴直线BC解析式y=x+3
设直线AB解析式y=mx+n
，
解得：m=﹣，n=3
∴直线AB解析式y=﹣x+3
（2）
∵折叠，点O与点B重合
∴DE是BO的垂直平分线
∴EO=BE，BD=OD
∴∠EBO=∠EOB，∠DBO=∠DOB
∵BO⊥CO
∴∠EBO+∠ECO=90°，∠EOB+∠EOC=90°
∴∠EOC=∠ECO
∴CE=EO
∴CE=BE
同理BD=DA
∴DE=
AC=6
∵点A（3，0），点B（0，3），点C（﹣9，0）
∴点E（﹣
，
），点D（，）
设点F（x，0）
∵△EFD是直角三角形，DE是斜边
∴DE2=EF2+DF2．
∴36=（x+）2+
+（x﹣
）2+
解得：x1=0，x2=﹣3
∴点F（0，0）或（﹣3，0）
（3）若BC为边，在BC上方和下方作正方形，如图：四边形BCFE是正方形，四边形BCMN是正方形
过点F作FH⊥AC于点H，过点E作EG⊥BO于点G
∵四边形BCFE是正方形
∴BC=CF，∠BCF=90°
∴∠BCO+∠FCH=90°，且∠FCH+∠CFH=90°
∴∠BCO=∠CFH且∠BOC=∠CHF=90°，BC=CF
∴△BCO≌△CFO（AAS）
∴CH=OB=3
，HF=CO=9
∴OH=9﹣3
∴点F（﹣9+3，﹣9）
同理可得△BEG≌△CBO
∴BG=CO=9，GE=BO=3
∴OG=9﹣3
∴点E（3，﹣9+3）
同理可得：点M（﹣9﹣3，9），点N（﹣3，9+3）
若BC为对角线，如图：四边形BECF是正方形
过点F作FM⊥CO于点M，作FN⊥BO于点 N
∵FM⊥CO，FN⊥BO，BO⊥CO
∴四边形OMFN是矩形
∴OM=FN，ON=FM
∵四边形BECF是正方形
∴CF=BF，∠CFB=90°
∵∠CFB=∠COB=90°
∴点C，点B，点O，点F四点共圆
∴∠FCO=∠OBF，且CF=BF，∠FMC=∠FNB=90°
∴△FMC≌△FNB（AAS）
∴FM=FN，CM=BN
∴边形FNOM是正方形
∴OM=ON=FM=FN
∵CM+OM=9，BN﹣ON=3
∴OM=ON=
，CM=BN=
∴点F（，）
同理可求点E坐标为（，）
