Question

【题目】如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为 ． （结果都保留π）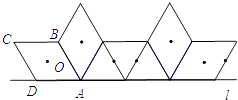

Answer 1

【答案】； nπ
【解析】解：∵菱形ABCD中，AB=2，∠C=60°，
∴△ABD是等边三角形，
BO=DO=1，
AO= = ，
第一次旋转的弧长= = ，
∵第一、二次旋转的弧长和= + = π，
第三次旋转的弧长为： =
∵3n÷3=n，
故经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为：n×（ π+ ）= nπ．
故答案为： ； nπ．

从图中可以看出，第一次旋转是以点A为圆心，那么菱形中心旋转的半径就是OA，解直角三角形可求出OA的长，圆心角是60°．第二次还是以点A为圆心，那么菱形中心旋转的半径就是OA，圆心角是60°．第三次就是以点B为旋转中心，OB为半径，旋转的圆心角为60度．旋转到此菱形就又回到了原图．故这样旋转3n次，就是这样的n个弧长的总长，依此计算即可得，进而得出经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长．