题目内容
在圆中,30°的圆周角所对的弦的长度为2 ,则这个圆的半径是________.
,则这个圆的半径是________.
2
分析:先求出弦所对的圆心角为60°,则可判断这条弦与两半径所组成的三角形是等边三角形,从而得出圆的半径.
解答:
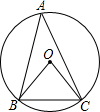
∵∠BAC=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
∴OB=OC=BC=2 ,即这个圆的半径为2
,即这个圆的半径为2 .
.
故答案为:2 .
.
点评:本题考查了圆周角定理,解答本题的关键是熟练掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.

分析:先求出弦所对的圆心角为60°,则可判断这条弦与两半径所组成的三角形是等边三角形,从而得出圆的半径.
解答:

∵∠BAC=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
∴OB=OC=BC=2
 ,即这个圆的半径为2
,即这个圆的半径为2 .
.故答案为:2
 .
.点评:本题考查了圆周角定理,解答本题的关键是熟练掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
