题目内容
已知抛物线![]() :
:![]() 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求![]() 的值;
的值;
(2)![]() 时,抛物线
时,抛物线![]() 向下平移
向下平移![]() 个单位后与抛物线
个单位后与抛物线![]() :
:![]() 关于
关于![]() 轴对称,且
轴对称,且![]() 过点
过点![]() ,求
,求![]() 的函数关系式;
的函数关系式;
(3)![]() 时,抛物线
时,抛物线![]() 的顶点为
的顶点为![]() ,且过点
,且过点![]() .问在直线
.问在直线![]() 上是否存在一点
上是否存在一点![]() 使得△
使得△![]() 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
解:当抛物线![]() 的顶点在
的顶点在![]() 轴上时
轴上时
![]()
解得![]() 或
或![]() ………………………………1分
………………………………1分
当抛物线![]() 的顶点在
的顶点在![]() 轴上时
轴上时
![]()
∴![]() ………………………………2分
………………………………2分
综上![]() 或
或![]() .
.
(2)当![]() 时,
时,![]()
抛物线![]() 为
为![]() .
.
向下平移![]() 个单位后得到
个单位后得到![]()
抛物线![]() 与抛物线
与抛物线![]() :
:![]() 关于
关于![]() 轴对称
轴对称
∴![]() ,
,![]() ,
,![]() …………………………………3分
…………………………………3分
∴抛物线![]() :
:![]()
∵![]() 过点
过点![]()
∴![]() ,即
,即![]() ……………………………………4分
……………………………………4分
解得![]() (由题意
(由题意![]() ,舍去)∴
,舍去)∴![]()
∴抛物线![]() :
:![]() .………………………………………………5分
.………………………………………………5分
(3)当![]() 时
时![]()
抛物线![]() :
:![]()
顶点![]()
∵过点![]()
∴![]()
∴![]() ………………6分
………………6分
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]()
直线![]() 的解析式为
的解析式为![]()
∴![]() ………………………………………7分
………………………………………7分
解析:略

练习册系列答案
相关题目
 :
: 的顶点在坐标轴上.
的顶点在坐标轴上. 的值;
的值; 时,抛物线
时,抛物线 个单位后与抛物线
个单位后与抛物线 :
: 关于
关于 轴对称,且
轴对称,且 ,求
,求 时,抛物线
时,抛物线 ,且过点
,且过点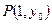 .问在直线
.问在直线 上是否存在一点
上是否存在一点 使得△
使得△ 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点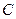 :
: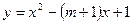 的顶点在坐标轴上.
的顶点在坐标轴上.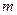 的值;
的值;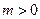 时,抛物线
时,抛物线 个单位后与抛物线
个单位后与抛物线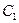 :
: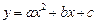 关于
关于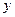 轴对称,且
轴对称,且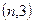 ,求
,求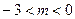 时,抛物线
时,抛物线 ,且过点
,且过点 .问在直线
.问在直线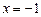 上是否存在一点
上是否存在一点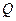 使得△
使得△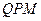 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点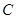 :
: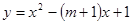 的顶点在坐标轴上.
的顶点在坐标轴上.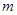 的值;
的值;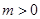 时,抛物线
时,抛物线 个单位后与抛物线
个单位后与抛物线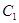 :
: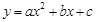 关于
关于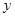 轴对称,且
轴对称,且 ,求
,求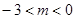 时,抛物线
时,抛物线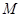 ,且过点
,且过点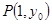 .问在直线
.问在直线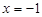 上是否存在一点
上是否存在一点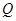 使得△
使得△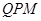 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点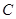 :
: 的顶点在坐标轴上.
的顶点在坐标轴上.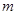 的值;
的值;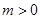 时,抛物线
时,抛物线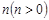 个单位后与抛物线
个单位后与抛物线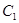 :
: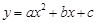 关于
关于 轴对称,且
轴对称,且 ,求
,求 时,抛物线
时,抛物线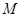 ,且过点
,且过点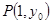 .问在直线
.问在直线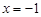 上是否存在一点
上是否存在一点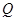 使得△
使得△ 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点