题目内容
【题目】如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．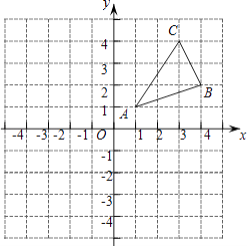
①画出△ABC关于y轴的对称图形△A1B1C1 ， 并写出B1点的坐标；
②画出△ABC绕原点O旋转180°后得到的图形△A2B2C2 ， 并写出B2点的坐标；
③在x轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．
【答案】解：△A1B1C1、△A2B2C2、△PAB如图所示，B1（﹣4，2）；B2（﹣4，﹣2）；P（2，0）．
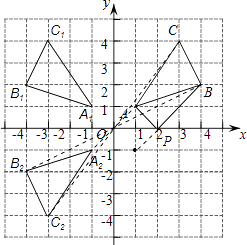
【解析】①分别作出点A、B、C关于y轴的对称点A1、B1、C1，然后顺次连接，并写出B1点的坐标。
（2）画出△ABC绕原点O旋转180°后得到的图形△A2B2C2，就是作出△ABC关于原点对称的△A2B2C2，并写出B2点的坐标。
（3）找出点A关于x轴的对称点A′，连接A′B与x轴相交于一点，根据轴对称确定最短路线问题，交点即为所求的点P的位置，然后连接AP、BP，根据图像写出点P的坐标即可。
【题目】第九届中国国际园林博览会（园博会）已于2013年5月18日在北京开幕，以下是根据近几届园博会的相关数据绘制的统计图的一部分：
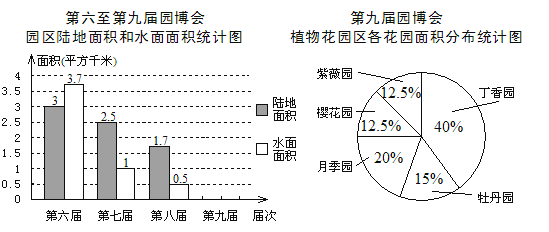
（1）第九届园博会的植物花园区由五个花园组成，其中月季园面积为0.04平方千米，牡丹园面积为 平方千米；
（2）第九届园博会园区陆地面积是植物花园区总面积的18倍，水面面积是第七、八两届园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据；
（3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位数量与日接待游客量和单日最多接待游客量中的某个量近似成正比例关系，根据小娜的发现，请估计将于2015年举办的第十届园博会大约需要设置的停车位数量（直接写出结果，精确到百位）。
第七届至第十届园博会游客量与停车位数量统计表
日均接待游客量（万人次） | 单日最多接待游客量（万人次） | 停车位数量（个） | |
第七届 | 0.8 | 6 | 约3 000 |
第八届 | 2.3 | 8.2 | 约4 000 |
第九届 | 8（预计） | 20（预计） | 约10 500 |
第十届 | 1.9（预计） | 7.4（预计） | 约 . |
