Question

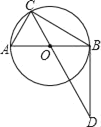
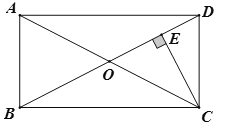
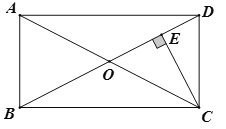
【题目】如图，在矩形中对角线与相交于点，，垂足为点，且，则的长为___________.

Answer 1

【答案】

【解析】

由矩形的性质可得OC＝OD，于是设DE＝x，则OE＝2x，OD＝OC＝3x，然后在Rt△OCE中，根据勾股定理即可得到关于x的方程，解方程即可求出x的值，进而可得CD的长，易证△ADC∽△CED，然后利用相似三角形的性质即可求出结果．

解：∵四边形ABCD是矩形，∴∠ADC＝90°，BD＝AC，OD＝BD，OC＝AC，∴OC＝OD，

∵EO＝2DE，∴设DE＝x，则OE＝2x，∴OD＝OC＝3x，

∵CE⊥BD，∴∠DEC＝∠OEC＝90°，

在Rt△OCE中，∵OE2+CE2＝OC2，∴（2x）2+52＝（3x）2，

解得：x＝，即DE＝，

∴，

∵∠ADE+∠CDE=90°，∠ECD+∠CDE=90°，∴∠ADE=∠ECD，

又∵∠ADC=∠CED=90°，∴△ADC∽△CED，

∴，即，解得：．

故答案为：．