题目内容
已知:如图①,正方形ABCD的边长是a,正方形AEFG的边长是b,且点F在AD上,连接DB,BF,(以下问题的结果可用a,b表示).(1)观察计算:△DBF的面积S=
(2)图形变式:
将图①中的正方形AEFG绕点A顺时针方向旋转45°得到图②,其他条件不变,请你求出图②中△DBF的面积S;
(3)探究发现:
当a>2b时,若把图①中的正方形AEFG绕点A旋转任意角度,在旋转过程中,△DBF的面积S是否能达到最大值、最小值?如果能达到,请画出图形,并求出最大值、最小值;如果达不到,请说明理由.(图③可用来画图).

分析:(1)根据DF=AD-AF,求三角形的底边DF,高为AB,根据三角形的面积公式计算;
(2)由正方形的性质可知AF∥BD,则△BDF与△BDA同底等高,根据S△DBF=S△DBA求面积;
(3)如图,在正方形ABCD外作正方形AEFG,此时,OF值最大,在正方形ABCD内作正方形AEFG,此时,OF最小,而BD=
a,分别计算OF的最大、最小值,求△DBF的面积的最大值、最小值.
(2)由正方形的性质可知AF∥BD,则△BDF与△BDA同底等高,根据S△DBF=S△DBA求面积;
(3)如图,在正方形ABCD外作正方形AEFG,此时,OF值最大,在正方形ABCD内作正方形AEFG,此时,OF最小,而BD=
| 2 |
解答:解:(1)∵AEFG是正方形,且边长是b,
∴Rt△AEF中,由勾股定理可求AF=
b,
∴DF=a-
b,
∴S△DBF=
DF•AB=
(a-
b)a=
a2-
ab;
(2)∵BD和AF分别是正方形ABCD与AEFG的对角线,
∴∠DBA=∠FAG=45°.
∴BD∥AF
∴S△DBF=S△DBA
又∵S△DBA=
BA•AD=
a2,
∴S△DBF=
a2;

(3)当a>2b时,存在最大值和最小值.
∵△BDF的底边BD=
a
∴当F点到BD的距离取得最大、最小值时,S△DBF取得最大值、最小值.
当点C、A、F三点在同一直线上时,如图③,
连接BF、DF,
S△DBF的最大值=
a(
a+
b)=
a2+ab,
S△DBF的最小值=
a(
a-
b)=
a2-ab.
∴Rt△AEF中,由勾股定理可求AF=
| 2 |
∴DF=a-
| 2 |
∴S△DBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)∵BD和AF分别是正方形ABCD与AEFG的对角线,
∴∠DBA=∠FAG=45°.
∴BD∥AF
∴S△DBF=S△DBA
又∵S△DBA=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DBF=
| 1 |
| 2 |

(3)当a>2b时,存在最大值和最小值.
∵△BDF的底边BD=
| 2 |
∴当F点到BD的距离取得最大、最小值时,S△DBF取得最大值、最小值.
当点C、A、F三点在同一直线上时,如图③,
连接BF、DF,
S△DBF的最大值=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
S△DBF的最小值=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
点评:本题考查了旋转的性质的运用,正方形的性质.关键是通过旋转确定三角形的底和高,发现三角形底和高的最大值和最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
23、已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.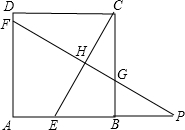 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点.
24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点. 已知:如图,在正方形ABCD中,P为对角线AC上的一动点,PE⊥AB于E,PF⊥BC于F,过点P作DP的垂线交BC于点G,DG交AC于点Q.下列说法:①EF=DP;②EF⊥DP;③
已知:如图,在正方形ABCD中,P为对角线AC上的一动点,PE⊥AB于E,PF⊥BC于F,过点P作DP的垂线交BC于点G,DG交AC于点Q.下列说法:①EF=DP;②EF⊥DP;③ F,BF与边CD交于点G,连接EG.设CE=x.
F,BF与边CD交于点G,连接EG.设CE=x.