Question

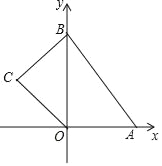
【题目】如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A的坐标为（6，0），点B的坐标为（0，8），点C的坐标为（﹣2，4），点M，N分别为四边形OABC边上的动点，动点M从点O开始，以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动，动点N从O点开始，以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动，点M，N同时从O点出发，当其中一点到达终点后，另一点也随之停止运动，设动点运动的时间t秒（t＞0），△OMN的面积为S．

（1）填空：AB的长是　 　，BC的长是　 ；

（2）当t=3时，求S的值；

（3）当3＜t＜6时，设点N的纵坐标为y，求y与t的函数关系式；

（4）若S=，请直接写出此时t的值．

Answer 1

【答案】（1）10，6（2）6（3）y=t（4）若S=，此时t的值8s或s或s

【解析】

试题分析:（1）利用勾股定理即可解决问题；

（2）如图1中，作CE⊥x轴于E．连接CM．当t=3时，点N与C重合，OM=3，易求△OMN的面积；

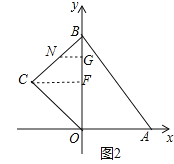
（3）如图2中，当3＜t＜6时，点N在线段BC上，BN=12﹣2t，作NG⊥OB于G，CF⊥OB于F．则F（0，4）．由GN∥CF，推出，即，可得BG=8﹣t，由此即可解决问题；

（4）分三种情形①当点N在边长上，点M在OA上时．②如图3中，当M、N在线段AB上，相遇之前．作OE⊥AB于E，则OE==，列出方程即可解决问题．③同法当M、N在线段AB上，相遇之后，列出方程即可；

试题解析：（1）在Rt△AOB中，∵∠AOB=90°，OA=6，OB=8，∴AB===10．

BC==6．

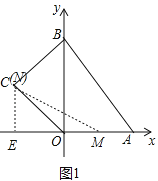
（2）如图1中，作CE⊥x轴于E．连接CM．

∵C（﹣，4），∴CE=4OE=，在Rt△COE中，OC===6，当t=3时，点N与C重合，OM=3，∴S△ONM=OMCE=×3×4=6，即S=6．

（3）如图2中，当3＜t＜6时，点N在线段BC上，BN=12﹣2t，作NG⊥OB于G，CF⊥OB于F．则F（0，4）．∵OF=4，OB=8，∴BF=8﹣4=4，∵GN∥CF，∴，即，∴BG=8﹣t，∴y=OB﹣BG=8﹣（8﹣t）=t．

（4）①当点N在边长上，点M在OA上时， tt=，解得t=（负根已经舍弃）．

②如图3中，当M、N在线段AB上，相遇之前．

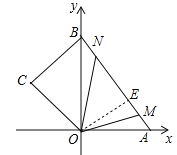
作OE⊥AB于E，则OE==，由题意 [10﹣（2t﹣12）﹣（t﹣6）] = ，解得t=8，同法当M、N在线段AB上，相遇之后．

由题意[（2t﹣12）+（t﹣6）﹣10] = ，解得t=．

综上所述，若S=，此时t的值8s或s或s．