Question

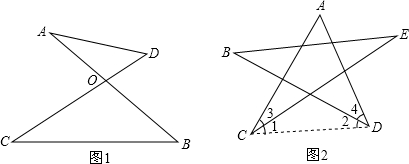
阅读材料：如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点O．
求证：S_{四边形ABCD}=ACBD；
证明：∵AC⊥BD，
∴S_{四边形ABCD}=S_△ACD+S_△ACB=AC*OD+AC*BO=AC（OD+OB）=AC*BD

解答下列问题：
（1）上述证明得到的结论可叙述为　                              　；
（2）如图2，在梯形ABCD中，AB∥CD，AD=BC，AC⊥BD，且AC=8，则S_梯形ABCD=　                　；
（3）如图3，在菱形ABCD中，AB=5，AC=8，则S_菱形ABCD=　                  ．

Answer 1

解：（1）根据题意得：对角线互相垂直的四边形的面积等于对角线乘积的一半．
（2）∵AB∥CD，AD=BC，
∴AC=BD=8，
∴S_梯形ABCD=×AC ×BD=×8×8=32
（3）∵四边形ABCD为菱形，
∴AC⊥BD，
AO=OC，
BO=DO，
在Rt△AOB中，AO=4，AB=5，
根据勾股定理得：BO=3，
∴BD=6，
∴S_菱形ABCD=×AC×BD=×6×8=24