Question

【题目】在平面直角坐标系中（单位长度为），已知点，，且．

（1）求，的值；

（2）若点是第一象限内一点，且轴，点到轴的距离为4，过点作轴的平行线，与轴交于点，点从点处出发，以每秒的速度沿直线向左移动，点从原点同时出发，以每秒的速度沿轴向右移动．

①经过几秒平行于轴？

②若某一时刻以，，，为顶点的四边形的面积是，求此时点的坐标．

Answer 1

【答案】（1），；（2）①，②（4，4）或（，4）

【解析】

（1）利用算术平方根和绝对值的非负性，即可求出答案；

（2）①设t秒后PQ平行于y轴，由于AP∥OQ，所以当AP=OQ时，四边形AOQP是平行四边形，那么PQ平行于y轴，根据AP=OQ列出关于t的方程，解方程即可；

②设t秒后四边形AOQP的面积为10cm2，分两种情况，根据四边形AOQP的面积=（OQ+AP）OA列出关于t的方程，进而求出点P的坐标．

解：（1）∵，

∴，

解得：；

（2）如图：

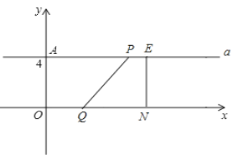
①当AP=QO时，PQ平行于y轴

∴，

解得：；

②分两种情况考虑；

如果P在第一象限

∴，

∴，

解得：，

∴AP=，

∴P的坐标（4，4）；

如果P在第二象限

∴，

∴，

∴，

∴，

∴P的坐标（，4）；