题目内容
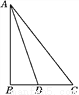
如图,在直角三角形ABC中,∠B=90°,AD平分∠BAC,交边BC于点D,如果BD=2,AC=6,那么△ADC的面积等于________.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
如图,在直角三角形ABC中,∠B=90°,AD平分∠BAC,交边BC于点D,如果BD=2,AC=6,那么△ADC的面积等于________.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案