题目内容
 反比例函数
反比例函数 的图象经过点A(2,4),B(m,2)
的图象经过点A(2,4),B(m,2)
(1)求k、m的值;
(2)如果M为X轴上一点,N为Y轴上一点,以点A、B、M、N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
解:(1)将A(2,4)代入反比例函数y= ,
,
得 =4,即k=8,
=4,即k=8,
解析式为y= ;
;
将B(m,2)代入y= 得
得 =2,m=4.
=2,m=4.
(2)设过A、B两点的解析式为y=kx+b,
将A(2,4),B(4,2)分别代入解析式为
 ,
,
解得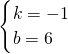 ;
;
解析式为y=-x+6.
已知MN∥AB,设过MN的直线为y=-x+n,
则N、M的坐标分别为N(0,n),M(n,0).
根据两点间的距离公式:n2+n2=(2-4)2+(4-2)2,
解得n=±2,
解析式为y=-x+2或y=-x-2.
分析:根据待定系数法求出k的值,再将B(m,2)代入解析式,转化为关于m的方程解答.
点评:本题考查了待定系数法和一次函数的性质及两点间距离公式解答,综合性较强,是一道好题.
 ,
,得
 =4,即k=8,
=4,即k=8,解析式为y=
 ;
;将B(m,2)代入y=
 得
得 =2,m=4.
=2,m=4.(2)设过A、B两点的解析式为y=kx+b,
将A(2,4),B(4,2)分别代入解析式为
 ,
,解得
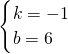 ;
;解析式为y=-x+6.
已知MN∥AB,设过MN的直线为y=-x+n,
则N、M的坐标分别为N(0,n),M(n,0).
根据两点间的距离公式:n2+n2=(2-4)2+(4-2)2,
解得n=±2,
解析式为y=-x+2或y=-x-2.
分析:根据待定系数法求出k的值,再将B(m,2)代入解析式,转化为关于m的方程解答.
点评:本题考查了待定系数法和一次函数的性质及两点间距离公式解答,综合性较强,是一道好题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知反比例函数的图象经过点P(1,-2),则这个函数的图象位于( )
| A、第一、三象限 | B、第二、三象限 | C、第二、四象限 | D、第三、四象限 |