题目内容
 已知:如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF⊥DG于F.
已知:如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF⊥DG于F.
求证:△AED≌△DFC.
证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°.
又∵AE⊥DG,CF⊥AE,
∴∠AED=∠DFC=90°,
∴∠EAD+∠ADE=∠FDC+∠ADE=90°,
∴∠EAD=∠FDC.
∴△AED≌△DFC(AAS).
分析:利用正方形的特性可知AD=DC,∠ADC=90°,再结合题中所给的有关角的等量关系可证明△AED≌△DFC.
点评:本题考查三角形全等的判定及正方形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
∴AD=DC,∠ADC=90°.
又∵AE⊥DG,CF⊥AE,
∴∠AED=∠DFC=90°,
∴∠EAD+∠ADE=∠FDC+∠ADE=90°,
∴∠EAD=∠FDC.
∴△AED≌△DFC(AAS).
分析:利用正方形的特性可知AD=DC,∠ADC=90°,再结合题中所给的有关角的等量关系可证明△AED≌△DFC.
点评:本题考查三角形全等的判定及正方形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
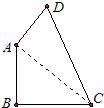 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.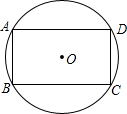 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.