题目内容
2.若A(-$\frac{7}{2}$,y1),B(-$\frac{3}{2}$,y2),C($\frac{1}{2}$,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是y2<y1<y3.分析 根据点A、B、C的横坐标结合二次函数图象上点的坐标特征分别求出y1、y2、y3的值,再比较大小即可得出结论.
解答 解:当x=-$\frac{7}{2}$时,y1=(-$\frac{7}{2}$)2+4×(-$\frac{7}{2}$)-5=-$\frac{27}{4}$;
当x=-$\frac{3}{2}$时,y2=(-$\frac{3}{2}$)2+4×(-$\frac{3}{2}$)-5=-$\frac{35}{4}$;
当x=$\frac{1}{2}$时,y3=($\frac{1}{2}$)2+4×$\frac{1}{2}$-5=-$\frac{11}{4}$.
∵-$\frac{35}{4}$<-$\frac{27}{4}$<-$\frac{11}{4}$,
∴y2<y1<y3.
故答案为:y2<y1<y3.
点评 本题考查了二次函数图象上点的坐标特征,根据点A、B、C的横坐标利用二次函数图象上点的坐标特征求出y1、y2、y3的值是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7.我县测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,31,35,36,34,31,对这组数据下列说法正确的是( )
| A. | 众数是31 | B. | 中位数是35 | C. | 平均数是32 | D. | 方差是6 |
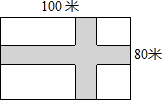 如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?
如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?