��Ŀ����
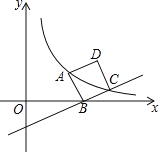
����Ŀ�����κ���ͼ���������ߣ���������ָƽ���ڵ�һ������![]() ��һ����ֱ��
��һ����ֱ��![]() ������ȵĵ�Ĺ켣�����ж���
������ȵĵ�Ĺ켣�����ж���![]() �������ߵĽ��㣬��ֱ��
�������ߵĽ��㣬��ֱ��![]() �������ߵ��ߣ�
�������ߵ��ߣ�
��������![]() (
(![]() )�Ľ���Ϊ
)�Ľ���Ϊ![]() �����磬������
�����磬������![]() �Ľ�����
�Ľ�����![]() ��������
��������![]() �Ľ�����___________��
�Ľ�����___________��
�ڽ�������![]() (
(![]() )����ƽ��
)����ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ(
����λ(![]() ��
��![]() )���ɵ�������
)���ɵ�������![]() �����������
�����������![]() �Ľ�����
�Ľ�����![]() �����磬������
�����磬������![]() �Ľ�����
�Ľ�����![]() ��������
��������![]() �Ľ�����_____________________���������ϲ��Ͻ���������⣺
�Ľ�����_____________________���������ϲ��Ͻ���������⣺
��1��������е���գ�
��2����֪���κ����Ľ���ʽΪ![]() ��
��
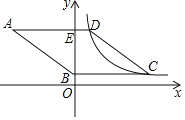
������ͼ��Ľ���![]() �����ꣻ
�����ꣻ
�������![]() ����
����![]() ��ƽ�е�ֱ������κ���
��ƽ�е�ֱ������κ���![]() ͼ������꣮
ͼ������꣮
���𰸡���1����![]() ����
����![]() ����2����
����2����![]() ����
����![]() ��
��![]()
��������
��1��ֱ�Ӹ����¶��弴����������ߵĽ��㣻
��2�����Ƚ����κ�������ʽ��ɶ���ʽ���ٸ����¶��弴����������ߵĽ��㣻
��������ɵõ�![]() ����
����![]() ��ƽ�е�ֱ�ߣ�����ƽ����x���ֱ���ϵĵ����������ȣ�����F��������������ʽ�������x��ֵ���Ӷ��ó��������꣮
��ƽ�е�ֱ�ߣ�����ƽ����x���ֱ���ϵĵ����������ȣ�����F��������������ʽ�������x��ֵ���Ӷ��ó��������꣮
��1���ٸ����¶��壬�ɵ�![]() ��
��
����������![]() �Ľ�����
�Ľ�����![]() ��
��
�ڸ����¶��壬�ɵ�h=1��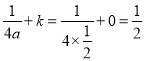 ��
��
����������![]() �Ľ�����
�Ľ�����![]() ��
��
��2���ٽ�![]() ��Ϊ����ʽ�ã�
��Ϊ����ʽ�ã�
![]()
�����¶��壬�ɵ�h=1��![]() ��
��
���Կɵ�������![]() �Ľ�������
�Ľ�������![]() ��
��
���ɢ�֪![]() �����Թ���
�����Թ���![]() ����
����![]() ��ƽ�е�ֱ����
��ƽ�е�ֱ����![]() ��
��
��![]() ����
����![]() �ã�
�ã�
![]() ��
��
��ã�![]() ��
��![]() ��
��
���ԣ�����![]() ����
����![]() ��ƽ�е�ֱ������κ���
��ƽ�е�ֱ������κ���![]() ͼ�������Ϊ
ͼ�������Ϊ![]() ��
��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�