题目内容
已知一次函数的图象经过点A(2,1),B(-1,-3),求此一次函数的图象与两坐标轴所围成的三角形面积.
解:设函数解析式为y=kx+b,
将两点代入可得: ,
,
解得: ,
,
∴函数解析式为:y= x-
x- .
.
当y=0,0= x-
x- ,
,
解得:x=
∴与x轴交点为( ,0),
,0),
当x=0,y=- ,
,
∴y轴交点为(0,- ),
),
∴一次函数的图象与两坐标轴所围成的三角形面积为:S= |x||y|=
|x||y|= ×
× ×
× =
=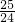 .
.
分析:假设函数解析式为y=kx+b,将两点代入可得出k和b的值,进而可得出函数解析式,再利用图象与坐标轴的交点坐标求出所围成的三角形面积即可.
点评:此题考查了待定系数法求函数解析式以及图象与坐标轴围成的三角形面积求法,注意掌握一次函数与坐标轴围成三角形的面积为= |x||y|,难度不大,注意在解答时要细心.
|x||y|,难度不大,注意在解答时要细心.
将两点代入可得:
 ,
,解得:
 ,
,∴函数解析式为:y=
 x-
x- .
.当y=0,0=
 x-
x- ,
,解得:x=

∴与x轴交点为(
 ,0),
,0),当x=0,y=-
 ,
,∴y轴交点为(0,-
 ),
),∴一次函数的图象与两坐标轴所围成的三角形面积为:S=
 |x||y|=
|x||y|= ×
× ×
× =
=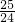 .
.分析:假设函数解析式为y=kx+b,将两点代入可得出k和b的值,进而可得出函数解析式,再利用图象与坐标轴的交点坐标求出所围成的三角形面积即可.
点评:此题考查了待定系数法求函数解析式以及图象与坐标轴围成的三角形面积求法,注意掌握一次函数与坐标轴围成三角形的面积为=
 |x||y|,难度不大,注意在解答时要细心.
|x||y|,难度不大,注意在解答时要细心. 
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标; 和反比例函数
和反比例函数 ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;