Question

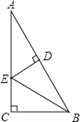
【题目】直线MN与直线PQ相交于O，点A在射线OP上，点B在射线OM上．

（1）如图1，已知AG、BG分别是∠BAO和∠ABO角的平分线，求的度数；

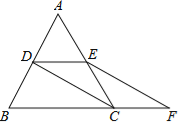
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，∠CED= 度；

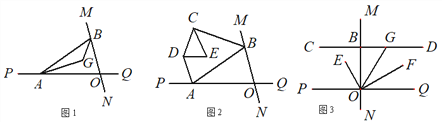
（3）如图3，，过点B作直线CD⊥MN，G为射线BD上一点，OF平分∠QOG，OE⊥OF，探索的大小是否发生变化？若不变，求其值；若改变，说明理由．

Answer 1

【答案】（1）；（2）50°；（3）比值为2，理由见解析.

【解析】分析：(1)根据三角形内角和定理，求得的度数，再利用角平分线的性质可得：即可求解；

（2）根据三角形内角和定理，求得的度数，再利用平角的定义可得：∠PAB+∠MBA＝360°－（），再由角角平分线的性质可得∠DAB+∠ABC＝，再根据三角形内角和定理即可求得∠CED的度数；

（3）设，由平行线的性质可得：∠QOG，再由角平分线的性质可得：∠GOF＝，由OE⊥OF可得∠BOG+∠GOF＝，由可得∠QOF+∠BOF＝，则有，则，则可求得它们的比值.

详解：

（1）∵，

∴，

又∵AG、BG平分、，

∴,

又∵+∠AGB＝，

∴∠AGB＝180－50＝130;

（2）∵，

∴，

∴∠PAB+∠MBA＝360°－（）=260,

又∵DE、CE分别是∠ADC和∠BCD的角平分线，

∴∠DAB+∠ABC＝＝130°，

又∵∠DAB+∠ABC+∠DEC＝180°（折叠前，这三个角是△ABE的内角）

∴∠DEC＝180°－130°＝50°.

（3）设

∵

∴CD∥PQ，

∴，

又∵OF平分，

∴，

又∵，

∴ ，

∴ ，

∴，不变化.