Question

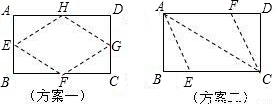
一次数学课上，老师让大家在一张长12cm、宽5cm的矩形纸片内，折出一个菱形．甲同学按照取两组对边中点的方法折出菱形EFGH（见方案一），乙同学沿矩形的对角线AC折出∠CAE=∠DAC，∠ACF=∠ACB的方法得到菱形AECF（见方案二），请你通过计算，比较这两种折法中，菱形面积较大的是（　　）

• A、甲
• B、乙
• C、甲乙相等
• D、无法判断

Answer 1

分析：方案一中，通过图可知四个小直角三角形全等，用矩形面积减去4个小直角三角形的面积，即可得菱形面积；方案二中，两个小直角三角形全等，设菱形边长为x，在直角三角形中利用勾股定理可求x，再利用底×高可求菱形面积．然后比较两者面积大小．

解答：解：方案一中，
∵E、F、G、H都是矩形ABCD的中点，
∴△HAE≌△HDG≌△FCG≌△FBE，
S_△HAE=

1

2

AE•AH=

1

2

×

1

2

AB×

1

2

AD=

1

2

×

1

2

×5×

1

2

×12=

15

2

，
S_菱形EFGH=S_矩形ABCD-4S_△HAE=12×5-

15

2

×4=30；

方案二中，设BE=x，则CE=AE=12-x，
∵AF=EC，AB=CD，AE=CF，
∴△ABE≌△CDF，
在Rt△ABE中，AB=5，BE=x，AE=12-x，由勾股定理得（12-x）²=5²+x²，解得x=

119

24

，
S_△ABE=

1

2

BE•AB=

1

2

×

119

24

×5=

595

48

，
S_菱形EFGH=S_矩形ABCD-2S_△ABE=12×5-

595

48

×2≈60-25=35＞30，
故甲＜乙．
故选B．

点评：本题考查了菱形面积的不同求法．