题目内容
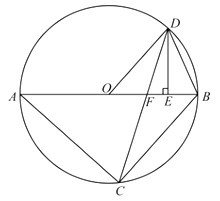
【题目】如图，已知 
内接于 
， 
是直径，点 
在 上， 
，过点 作 
，垂足为 
，连接 
交 
边于点 
．
（1）求证： 
∽ ；
（2）求证： 
；
（3）连接 
，设 的面积为 
，四边形 
的面积为 
，若 
，求 
的值．
【答案】
（1）
证明：∵AB是圆O的直径，
∴∠ACB=90°，
∵DE⊥AB，
∴∠DEO=90°，
∴∠DEO=∠ACB，
∵OD//BC，
∴∠DOE=∠ABC，
∴△DOE~△ABC，
（2）
证明：∵△DOE~△ABC，
∴∠ODE=∠A，
∵∠A和∠BDC是弧BC所对的圆周角，
∴∠A=∠BDC，
∴∠ODE=∠BDC，
∴∠ODF=∠BDE。
（3）
解：因为△DOE~△ABC ,
所以
，
即
=4
=4
因为OA=OB，
所以
=
，即=2,
因为
=
,S2=++
=2S1+S1+,
所以=
，
所以BE=
OE,即OE=
OB=OD，
所以sinA=sin∠ODE=
=
【解析】（1）易证∠DEO=∠ACB=90°和∠DOE=∠ABC，根据“有两对角相等的两个三角形相似”判定△DOE~△ABC；
（2）由△DOE~△ABC，可得∠ODE=∠A，由∠A和∠BDC是弧BC所对的圆周角，则∠A=∠BDC，从而通过角的等量代换即可证得；
（3）由∠ODE=∠A，可得sinA=sin∠ODE=
=
；而由△DOE~△ABC ,可得
， 即
=4
=4
=
， 即=2,又因为
=
,S2=+
+
=2S1+S1+,则可得=
， 可求得OE与OB的比值.
【考点精析】认真审题，首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)，还要掌握相似三角形的性质(对应角相等，对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键．
