��Ŀ����
����Ŀ��һ���н�ˮ�����ˮ�ܵ���������ijʱ�̿�ʼ![]() ������ֻ��ˮ����ˮ��������
������ֻ��ˮ����ˮ��������![]() �����ڼȽ�ˮ�ֳ�ˮ��ֱ�������ڵ�ˮ���ﵽ
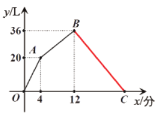
�����ڼȽ�ˮ�ֳ�ˮ��ֱ�������ڵ�ˮ���ﵽ![]() ����ͼ������ϵ�е����߶�
����ͼ������ϵ�е����߶�![]() ��ʾ��һ�����������ڵ�ˮ��
��ʾ��һ�����������ڵ�ˮ��![]() ����λ��
����λ��![]() ����ʱ��
����ʱ��![]() ����λ���֣�֮��Ĺ�ϵ��
����λ���֣�֮��Ĺ�ϵ��
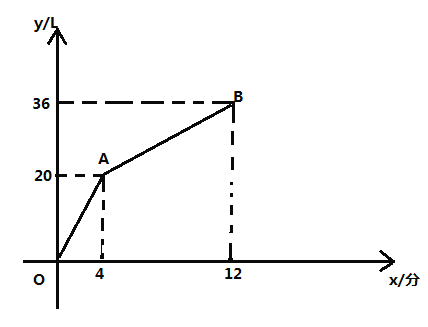
��1����������ˮ�ܣ�ÿ���ӿɽ�ˮ________![]() ��
��
��2�����ˮ�����ˮ��ͬʱ��ʱ�����ڵ�ˮ��![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ![]() ��
��
��3���������ڵ�ˮ���ﵽ![]() ʱ�����̹رս�ˮ�ܣ�ֱ�������ڵ�ˮȫ�����꣮����ͬһ����ϵ�л�����ʾ��ˮ�����������ڵ�ˮ��
ʱ�����̹رս�ˮ�ܣ�ֱ�������ڵ�ˮȫ�����꣮����ͬһ����ϵ�л�����ʾ��ˮ�����������ڵ�ˮ��![]() ��ʱ��
��ʱ��![]() ��ϵ���߶�
��ϵ���߶�![]() ����ֱ��д����
����ֱ��д����![]() �����꣮
�����꣮
���𰸡���1��![]() ����2��
����2��![]()
![]() ����3����
����3����![]() ������Ϊ
������Ϊ![]() ��
��
��������
��1������4����ˮ���ﵽ![]() ������⣻
������⣻
��2����![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
![]() �����ô���ϵ����������⣻
�����ô���ϵ����������⣻
��3�������ˮ��ÿ���ӵij�ˮ��������������ڵ�ˮȫ�������ʱ�䣬�õ�C�����꼴����ͼ��
��1����������ˮ�ܣ�ÿ���ӿɽ�ˮ20��4=![]()
![]()
�ʴ�Ϊ��5��
��2����![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��![]() ����
����![]() ��
�У�
��![]()
�⣬��![]() ��
��
���ԣ�![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
![]() ��
��
��3�����ˮ��ÿ���ӵij�ˮ��Ϊa��
����ɵã�12-4������5-a��=36-20
���a=3
�������ڵ�ˮȫ�������ʱ��Ϊ36��3=12�����ӣ�
��C![]()
��ͼ���߶�![]() ��Ϊ����
������