题目内容
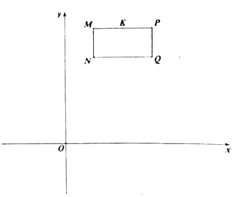
【题目】如图，在平面直角坐标中，点
的坐标为
，点
的坐标为
，将线段
向右平移
个单位长度得到线段
（点
和点
分别是点和点的对应点），连接
、
，点
是线段的中点.
备用图
（1）求点的坐标；
（2）若长方形
以每秒
个单位长度的速度向正下方运动，（点
、
、
、
、
分别是点、、、、的对应点），当
与
轴重合时停止运动，连接
、
，设运动时间为
妙，请用含的式子表示三角形
的面积
（不要求写出的取值范围）；
（3）在（2）的条件下，连接
、
，问是否存在某一时刻，使三角形
的面积等于三角形的面积？若存在，请求出值；若不存在，请说明理由.
【答案】（1）
（2）
（3）存在，
，
，见解析.
【解析】
（1）根据M和N的坐标和平移的性质可知：MN∥y轴∥PQ，根据K是PM的中点可得K的坐标；
（2）根据题意可知，AE=2，AE边上的高是
，由三角形面积公式可得三角形OAE的面积S；
（3）存在两种情况：
①如图2，当点B在OD上方时
②如图3，当点B在OD上方时，
过点B作BG⊥x轴于G，过D作DH⊥x轴于H，分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论．
解：（1）由题意可知
，
是线段
的中点，
，
，
；
（2）如图所示，延长
交
轴于点
则
，
；
（3）①如图，当点
在
上方时，
过点作
轴，垂足为
过点
作
轴，垂足为
则
，
，
，
，
，
，
，
，
，
，
；
②如图，当点在下方
过点作轴，垂足为
过点作轴，垂足为
则，
，
，，，，
，
，
，
，
，
，
.
故答案为：（1）（2）（3）存在，，，见解析.
【题目】某服装店用4400元购进A，B两种新式服装，按标价售出后可获得毛利润2800元（毛利润＝售价﹣进价），这两种服装的进价，标价如表所示．
类型价格 | A型 | B型 |
进价（元/件） | 60 | 100 |
标价（元/件） | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数；
(2)如果A种服装按标价的9折出售，B种服装按标价的8折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？
