题目内容
直线l1:y=(m-2)x-2与直线l2:y=-
x平行,则m的值是
;直线l1向上平移
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
2
2
个单位就可得到直线l2.分析:根据两直线平行的问题得到m-2=-
,解得m=
,然后根据一次函数的几何变换得到把y=-
x-2向上平移2个单位就可得到直线y=-
x.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵直线l1:y=(m-2)x-2与直线l2:y=-
x平行,
∴m-2=-
,
∴m=
∴直线l1:y=-
x-2向上平移2个单位就可得到直线l2.
故答案为:
,2.
| 1 |
| 2 |
∴m-2=-
| 1 |
| 2 |
∴m=
| 3 |
| 2 |
∴直线l1:y=-
| 1 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了两直线相角或平行问题:若两直线平行,则一次项系数相等;若两直线相交,则两直线的解析式所组的方程组的解为交点坐标.也考查了一次函数图象与几何变换.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,三条直线L1,L2,L3相交于一点O,若∠1=
如图,三条直线L1,L2,L3相交于一点O,若∠1= 如图,直线l1:y=-x+1和直线l2:
如图,直线l1:y=-x+1和直线l2: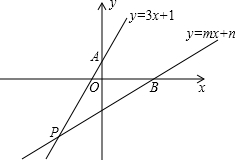 如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题: (2013•启东市一模)如图,直线l1∥l2,∠1=40°,∠2=75°,则∠3=
(2013•启东市一模)如图,直线l1∥l2,∠1=40°,∠2=75°,则∠3= 如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )
如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )