题目内容
梯形ABCD中，AD∥BC，AD=a，BC=b，EF∥AD交AB，CD于E，F，且梯形AEFD与梯形EBCF相似，则EF等于
- A.
- B.
- C.
- D.不能确定
A
分析：利用相似多边形的对应边的比相等，对应角相等分析．
解答：梯形AEFD与梯形EBCF相似，
则对应边的比相等，
因而得到：AD：EF=EF：BC
即a：EF=EF：b，
则EF2=ab
∴EF=．
故选A．
点评：本题主要考查了相似形的性质，对应边的比相等．
分析：利用相似多边形的对应边的比相等，对应角相等分析．
解答：梯形AEFD与梯形EBCF相似，
则对应边的比相等，
因而得到：AD：EF=EF：BC
即a：EF=EF：b，
则EF2=ab
∴EF=
．故选A．
点评：本题主要考查了相似形的性质，对应边的比相等．
练习册系列答案
名校课堂系列答案
相关题目
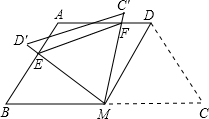如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
DE．
如图，在梯形ABCD中，AD∥BC，AB=CD，点E在BC的延长线上，且∠BDE=∠ADC．求证：AB•BD=DE•AD．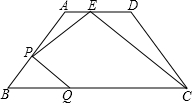
如图，在等腰梯形ABCD中，AD∥BC，AB=5，AD=6，BC=12，点E在AD边上，且AE：ED=1：2，点P是AB边上的一个动点，（P不与A，B重合）过点P作PQ∥CE交BC于点Q，设AP=x，CQ=y，则y与x之间的函数关系是
分别交边CD、BC于点F、E，若AD=3，BC=12，