Question

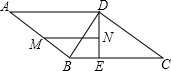（1997•四川）已知：如图，BD是?ABCD的对角线，∠ABD=90°，DE⊥BC，垂足为E，M，N分别是AB、DE的中点，tanC=

1

2

，S_△BCD=9cm²．求MN的长（不取近似值）．

Answer 1

分析：根据四边形ABCD是平行四边形，得出∠BDC=∠ABD=90°，根据tanC=

1

2

，得出

BD

CD

=

1

2

，设BD=xcm，则CD=2xcm，根据S_△BCD=

1

2

•x•2x=9，求出 x的值，从而得出BD、CD的长，在Rt△BDC中，求出BC=

BD2+CD2

，再根据AD=BC，求出AD，根据Rt△BED∽Rt△BDC，得出

BE

BD

=

BD

BC

，BE=

BD2

BC

，最后根据M、N分别是AB、DE的中点，得出MN=

AD+BE

2

即可求出答案．．

解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD
∴∠BDC=∠ABD=90°，
∵tanC=

1

2

，
∴

BD

CD

=

1

2

，
设BD=xcm，则CD=2xcm，
∴S_△BCD=

1

2

•x•2x=9（cm）²
解得  x=3（cm）
∴BD=3cm，CD=2x=2×3=6（cm），
在Rt△BDC中，由勾股定理，得
BC=

BD2+CD2

=

32+62

=3

5

（cm），
又∵AD=BC，
∴AD=3

5

（cm）
∵DE⊥BC，
∴Rt△BED∽Rt△BDC
∴

BE

BD

=

BD

BC

，
∴BE=

BD2

BC

=

32

3 5

=

3

5

5

（cm）
又∵AD∥BE，AB与DE不平行，
∴四边形ABED是梯形．
∵M、N分别是AB、DE的中点，
∴MN=

AD+BE

2

=

3 5 + 3 5 5

2

=

9

5

5

（cm）．

点评：此题考查了相似三角形的判定与性质，用到的知识点是相似三角形的判定与性质、勾股定理、平行四边形的性质，关键是运用有关性质和定理，列出算式，求出线段的长度．