题目内容
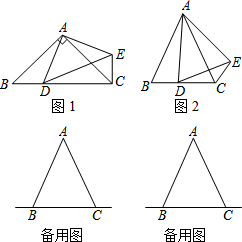 已知:在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
已知:在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE. (1)如图1,当点D在线段BC上,如果∠BAC=90°,发现
①△
②∠BCE=
(2)设∠BAC=x,∠BCE=y.
①如图2,当点D在线段BC上移动,则x,y之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则x,y之间有怎样的数量关系?请直接写出你的结论.
考点:全等三角形的判定与性质
专题:
分析:(1)问要求∠BCE的度数,可将它转化成与已知角有关的联系,根据已知条件和全等三角形的判定定理,得出△ABD≌△ACE,再根据全等三角形中对应角相等,最后根据直角三角形的性质可得出结论;
(2)①问在第(1)问的基础上,将α+β转化成三角形的内角和;
②问是第(1)问和第①问的拓展和延伸,要注意分析两种情况.
(2)①问在第(1)问的基础上,将α+β转化成三角形的内角和;
②问是第(1)问和第①问的拓展和延伸,要注意分析两种情况.
解答:解:(1)当点D在线段BC上,如果∠BAC=90°,发现
①△ABD≌△ACE,
②∠BCE=90度;
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
又∵∠BAC=90°
∴∠BCE=90°;
(2)①x+y=180°,
理由:∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=y,
∵x+∠B+∠ACB=180°,
∴x+y=180°;
②当点D在射线BC上时,x+y=180°;
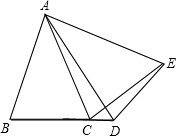
理由:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠BAC+∠ABD+∠BCA=180°,
∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,
∴x+y=180°;
当点D在射线BC的反向延长线上时,x=y.
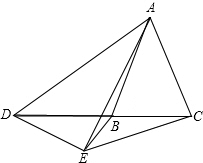
理由:∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE,
∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,
∴∠BAC=∠BCE,
即x=y.
①△ABD≌△ACE,
②∠BCE=90度;
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
又∵∠BAC=90°
∴∠BCE=90°;
(2)①x+y=180°,
理由:∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=y,
∵x+∠B+∠ACB=180°,
∴x+y=180°;
②当点D在射线BC上时,x+y=180°;

理由:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠BAC+∠ABD+∠BCA=180°,
∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,
∴x+y=180°;
当点D在射线BC的反向延长线上时,x=y.

理由:∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
在△ADB和△AEC中,
|
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE,
∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,
∴∠BAC=∠BCE,
即x=y.
点评:本题考查三角形全等的判定,以及全等三角形的性质;两者综合运用,促进角与角相互转换,将未知角转化为已知角是关键.本题的亮点是由特例引出一般情况.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
在电视访谈节目中,一位气象专家说“本地区未来10天内发生降水的概率是三分之二”,以下哪个选项最能反映气象专家的意思( )
| A、这个地区从现在开始经过6至7天会发生降水 |
| B、这个地区未来10天内将会发生一次降水 |
| C、这个地区未来10天内发生降水比不发生降水的可能性大 |
| D、我们不能判断何时会有降水发生 |
若正方形的对角线长为8cm,则这个正方形的面积为( )
| A、32cm2 | ||
| B、64cm2 | ||
C、8
| ||
D、32
|
 如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.
如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.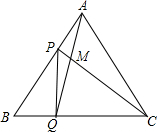 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第 已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.
已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.