��Ŀ����
��2011���ຣ��28,12����֪һԪ���η���x2��4x��3=0��������m��n��m��n.��ͼ12����������y=-x2+bx+c��ͼ����A��m��0����B��0��n��.
��1���������ߵĽ���ʽ.
��2������1���е���������x�����һ������ΪC.����ͼ��ش𣬵�xȡ��ֵʱ�������ߵ�ͼ����ֱ��BC���Ϸ���
��3����P���߶�OC�ϣ���PE��x���������߽����E����ֱ��BC����CPE������ֳ���ȵ������֣����P������.

��1����x2��4x+3=0��������Ϊ x1=1,x2=3
��A���������1,0����B���������0,3��
�֡�������y=��x2+bx+c��ͼ����A��1,0����B��0,3������

�������ߵĽ���ʽΪ y=��x2-2x+3
��2����ֱ��BC

�ɣ�1���ã�y=��x2-2x+3
�� ������y=��x2��2x+3��x�����һ������ΪC �x2��2x+3=0
��ã�x1=1��x2=��3
��C�����������3,0��
��ͼ��֪������3��x��0ʱ�������ߵ�ͼ����ֱ��BC���Ϸ�.
(3)��ֱ��BC��PE��F��P������Ϊ��a,0��,��E������Ϊ��a����a2��2a+3��
��ֱ��BC����CPE������ֳ���ȵ�������.
��F���߶�PE���е�.
��F��������ǣ�a�� ��
��
��ֱ��BC����B��0.3����C(-3,0)
��ֱ��BC�Ľ���ʽΪy=x+3
�ߵ�F��ֱ��BC�ϣ����Ե�F����������ֱ��BC�Ľ���ʽ
�� =a+3
=a+3
��� a1=��1,a2=��3(��ʱP�����C�غϣ���ȥ)
��P��������ǣ���1,0������:
��
��A���������1,0����B���������0,3��
�֡�������y=��x2+bx+c��ͼ����A��1,0����B��0,3������

�������ߵĽ���ʽΪ y=��x2-2x+3
��2����ֱ��BC

�ɣ�1���ã�y=��x2-2x+3
�� ������y=��x2��2x+3��x�����һ������ΪC �x2��2x+3=0
��ã�x1=1��x2=��3
��C�����������3,0��
��ͼ��֪������3��x��0ʱ�������ߵ�ͼ����ֱ��BC���Ϸ�.
(3)��ֱ��BC��PE��F��P������Ϊ��a,0��,��E������Ϊ��a����a2��2a+3��
��ֱ��BC����CPE������ֳ���ȵ�������.
��F���߶�PE���е�.
��F��������ǣ�a��
 ��
����ֱ��BC����B��0.3����C(-3,0)
��ֱ��BC�Ľ���ʽΪy=x+3
�ߵ�F��ֱ��BC�ϣ����Ե�F����������ֱ��BC�Ľ���ʽ
��
 =a+3
=a+3��� a1=��1,a2=��3(��ʱP�����C�غϣ���ȥ)
��P��������ǣ���1,0������:
��

��ϰ��ϵ�д�
�����Ŀ
 ��������Գ�ͼ�Σ��������������ļ���ͼ�Σ�����
��������Գ�ͼ�Σ��������������ļ���ͼ�Σ����� �� ������Բ�������ȱ������Σ������߶Σ�Ϊ��������˼һ�����أ����������Գ�ͼ�Σ���д��һ���Ҫ�Ľ�˵�ʡ�
�� ������Բ�������ȱ������Σ������߶Σ�Ϊ��������˼һ�����أ����������Գ�ͼ�Σ���д��һ���Ҫ�Ľ�˵�ʡ�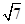 ���к�
���к� ���ĸ�ʵ���У��������ǣ� ��
���ĸ�ʵ���У��������ǣ� ��
 �У��Ա���x��ȡֵ��Χ��
��
�У��Ա���x��ȡֵ��Χ��
��