题目内容
如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t<5).解答下列问题:(1)试判断△PEF的形状,并请说明理由.
(2)当0<t<2.5时,设△PEQ的面积为y(cm2),求出y(cm2)与t(s)之间的函数关系式.

【答案】分析:(1)根据条件可以得出△AEP≌△CPF,从而得出PE=PF,就可以得出得出△PEF的形状为等腰三角形;
(2)作PG⊥EF于G,就可以而出EG=3,由AB∥EF就可以得出 就可以表示出EQ,近而表示出GQ和PQ,在Rt△PGQ中由勾股定理就可以表示出PG,根据三角形的面积公式就可以求出y与t的关系式.
就可以表示出EQ,近而表示出GQ和PQ,在Rt△PGQ中由勾股定理就可以表示出PG,根据三角形的面积公式就可以求出y与t的关系式.
解答:解:(1)△PEF为等腰三角形,
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,AB∥CD,
∴∠DAC=∠BCA.
∵AE=BF=CP=t,
∴CF=DE.
∵AD=AC,
∴AC=BC,
∴AP=CF.
∵在△AEP和△CPF中,
 ,
,
∴△AEP≌△CPF(SAS),
∴EP=PF.
∴△PEF为等腰三角形;
(2)作PG⊥EF于G,
∴EG= EF.
EF.
∵AE∥BF,AB∥EF,
∴四边形ABFE是平行四边形,
∴AB=EF.
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴ ,
,
∴ ,
,
∴EQ= t,
t,
∴GQ=3- t.
t.
∵CP=AQ=t,
∴PQ=5-2t,
在Rt△PGQ中,由勾股定理,得
PG= ,
,
=4- t.
t.
∵S△PQE= EQ•PG,
EQ•PG,
∴y= ×
× t×(4-
t×(4- t),
t),
=- t2+
t2+ t(0<t<2.5).
t(0<t<2.5).
∴y与t之间的函数关系式为:y=- t2+
t2+ t(0<t<2.5).
t(0<t<2.5).
点评:本题考查了平行四边形的性质的运用,等腰三角形的判定及性质的运用,勾股定理的运用,平行线分线段成比例定理的运用,三角形的面积公式的运用,解答时运用相似表示出EQ的值和运用勾股定理表示PG的值是解答本题的难点和关键.
(2)作PG⊥EF于G,就可以而出EG=3,由AB∥EF就可以得出
 就可以表示出EQ,近而表示出GQ和PQ,在Rt△PGQ中由勾股定理就可以表示出PG,根据三角形的面积公式就可以求出y与t的关系式.
就可以表示出EQ,近而表示出GQ和PQ,在Rt△PGQ中由勾股定理就可以表示出PG,根据三角形的面积公式就可以求出y与t的关系式.解答:解:(1)△PEF为等腰三角形,
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,AB∥CD,
∴∠DAC=∠BCA.
∵AE=BF=CP=t,
∴CF=DE.
∵AD=AC,
∴AC=BC,
∴AP=CF.
∵在△AEP和△CPF中,
 ,
,∴△AEP≌△CPF(SAS),
∴EP=PF.
∴△PEF为等腰三角形;
(2)作PG⊥EF于G,
∴EG=
 EF.
EF.∵AE∥BF,AB∥EF,
∴四边形ABFE是平行四边形,
∴AB=EF.
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴
 ,
,
∴
 ,
,∴EQ=
 t,
t,∴GQ=3-
 t.
t.∵CP=AQ=t,
∴PQ=5-2t,
在Rt△PGQ中,由勾股定理,得
PG=
 ,
,=4-
 t.
t.∵S△PQE=
 EQ•PG,
EQ•PG,∴y=
 ×
× t×(4-
t×(4- t),
t),=-
 t2+
t2+ t(0<t<2.5).
t(0<t<2.5).∴y与t之间的函数关系式为:y=-
 t2+
t2+ t(0<t<2.5).
t(0<t<2.5).点评:本题考查了平行四边形的性质的运用,等腰三角形的判定及性质的运用,勾股定理的运用,平行线分线段成比例定理的运用,三角形的面积公式的运用,解答时运用相似表示出EQ的值和运用勾股定理表示PG的值是解答本题的难点和关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=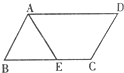 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.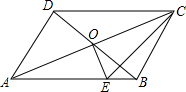 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是