题目内容
如图，在直角坐标系中有一个半径为r的圆A，圆心A在x轴的正半轴上，从坐标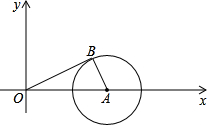
原点O向圆A作切线，切点是B．（1）如果OB=3
| 3 |
（2）设∠AOB=α，在图中确定一个与2α大小相等的角（可以添加辅助线），并说明理由；
（3）在（2）的基础上，试探究sin2α与2sinα是否相等．如果相等，请说明理由；如果不相等，请你找出它们之间正确的关系式．
分析：（1）根据题意设出圆的半径为r，根据切线的性质，勾股定理即可推出r的长度，即可推出A点的坐标，
（2）作辅助线，取OA的中点D，过点D作OA的垂线，交OB于点C，连接AC，则OC=AC，推出∠ACB=∠AOC+∠CAO=2α，
（3）根据（1）和（2）推出的结论，即得：sinα=
，cosα=
，sin2α=
，然后根据△ABO∽△CDO，推出OC=
，由OD=
OA，推出sin2α=2•
•
=2cosα•sinα．
（2）作辅助线，取OA的中点D，过点D作OA的垂线，交OB于点C，连接AC，则OC=AC，推出∠ACB=∠AOC+∠CAO=2α，
（3）根据（1）和（2）推出的结论，即得：sinα=
| AB |
| OA |
| OB |
| OA |
| AB |
| AC |
| OD•OA |
| OB |
| 1 |
| 2 |
| OB |
| OA |
| AB |
| OA |
解答：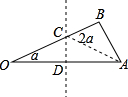
解：（1）AB=r，OB=3
，OA=r+3，
∵OB与圆A相切，
∴AB⊥BO，
∴∠ABO=90°，
在Rt△OAB中，OA2=AB2+OB2，
∴(r+3)2=r2+(3
)2，
∴r=3，
∴A（6，0），
∴sin∠AOB=
=
，
（2）如图，取OA的中点D，过点D作OA的垂线，交OB于点C，连接AC，
∵DC是OA的垂直平分线，
∴OC=AC，
∴∠COA=∠CAO=α，
∴∠ACB=∠AOC+∠CAO=2α．
（3）由（1）可知∠B=90°，
∴在Rt△ABO中sinα=
，cosα=
，
由（2）可知DC⊥OA，
∴∠CDO=90°在Rt△ABC中sin2α=
，
在Rt△ABO和Rt△CDO中，∠O=∠O，∠CDO=∠B，
∴△ABO∽△CDO，
∴
=
，
∴OC=
，
∵OD=
OA，且OC=AC，
∴AC=
=
，
∴sin2α=
=
=
=2•
•
=2cosα•sinα．
解：（1）AB=r，OB=3| 3 |
∵OB与圆A相切，
∴AB⊥BO，
∴∠ABO=90°，
在Rt△OAB中，OA2=AB2+OB2，
∴(r+3)2=r2+(3
| 3 |
∴r=3，
∴A（6，0），
∴sin∠AOB=
| AB |
| OA |
| 1 |
| 2 |
（2）如图，取OA的中点D，过点D作OA的垂线，交OB于点C，连接AC，
∵DC是OA的垂直平分线，
∴OC=AC，
∴∠COA=∠CAO=α，
∴∠ACB=∠AOC+∠CAO=2α．
（3）由（1）可知∠B=90°，
∴在Rt△ABO中sinα=
| AB |
| OA |
| OB |
| OA |
由（2）可知DC⊥OA，
∴∠CDO=90°在Rt△ABC中sin2α=
| AB |
| AC |
在Rt△ABO和Rt△CDO中，∠O=∠O，∠CDO=∠B，
∴△ABO∽△CDO，
∴
| OD |
| OB |
| OC |
| OA |
∴OC=
| OD•OA |
| OB |
∵OD=
| 1 |
| 2 |
∴AC=
| ||
| OB |
| OA2 |
| 2OB |
∴sin2α=
| AB |
| AC |
| AB | ||
|
| 2OB•AB |
| OA2 |
| OB |
| OA |
| AB |
| OA |
点评：本题主要考查相似三角形的判定与性质，解直角三角形，切线的性质，勾股定理的运用，全等三角形的判定与性质，关键在于熟练并正确地运用各性质定理，认真进行等量代换．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：