题目内容
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1350,得到矩形EFGH(点E与O重合).

(1)若GH交y轴于点M,则∠FOM= ,OM= ;
(2)矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤ 时,S与t之间的函数关系式.
时,S与t之间的函数关系式.

(1)若GH交y轴于点M,则∠FOM= ,OM= ;
(2)矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤
 时,S与t之间的函数关系式.
时,S与t之间的函数关系式.(1)450, ;(2)①
;(2)① -2;②
-2;②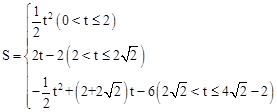 .
.
 ;(2)①
;(2)① -2;②
-2;②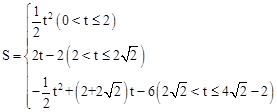 .
.试题分析:(1)由旋转的性质,得∠AOF=1350,∴∠FOM=450,由旋转的性质,得∠OHM=450,OH=OC=2,∴OM=
 ;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI=
;(2)①由矩形的性质和已知AD∥BO,可得四边形ABOD是平行四边形,从而DO=AB=2,又由△DOI是等腰直角三角形可得OI=OD=2,从而由平移的性质可求得t=IM=OM-OI= -2;②首先确定当0<t≤
-2;②首先确定当0<t≤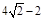 时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤
时,矩形EFGH沿y轴向上平移过程中关键点的位置,分0<t≤2,2<t≤ ,
, <t≤
<t≤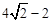 三种情况求出S与t之间的函数关系式.
三种情况求出S与t之间的函数关系式.试题解析:(1)450;
 .
.(2)①如图1,设直线HG与y轴交于点I,
∵四边形OABC是矩形,∴AB∥DO,AB=OC.
∵C(2,0),∴AB=OC=2.
又∵AD∥BO, ∴四边形ABOD是平行四边形. ∴DO=AB=2.
由(1)易得,△DOI是等腰直角三角形,∴OI=OD=2.
∴t=IM=OM-OI=
 -2.
-2.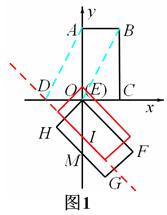
②如图2,
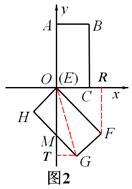
过点F,G分别作x轴,y轴的垂线,垂足为R,T,连接OC. 则
由旋转的性质,得,OF=OA=4,∠FOR=450,
∴OR=RF=
 ,F(
,F( ,-
,- ).
).由旋转的性质和勾股定理,得OG=
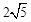 ,
,设TG=MT=x,则OT=OM+MT=
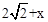 .
.在Rt△OTG中,由勾股定理,得
 ,解得x=
,解得x=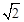 . ∴G(
. ∴G(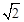 ,-
,-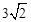 ).
).∴用待定系数法求得直线FG的解析式为
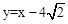 .
.当x=2时,
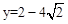 .
.∴当t=
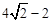 时,就是GF平移到过点C时的位置(如图5).
时,就是GF平移到过点C时的位置(如图5).∴当0<t≤
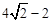 时,几个关键点如图3,4,5所示:
时,几个关键点如图3,4,5所示:如图3 ,t=OE=OC=2,此时,矩形EFGH沿y轴向上平移过程中边EF经过点C;
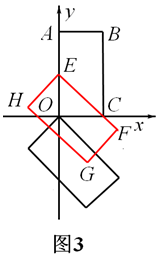
如图4,t=OE=OM=
 ,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;
,此时,矩形EFGH沿y轴向上平移过程中边HG经过点O;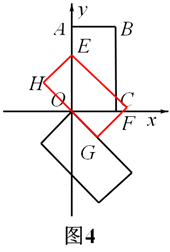
如图5,t=OE=
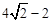 ,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.
,此时,矩形EFGH沿y轴向上平移过程中边FG经过点C.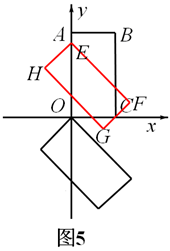
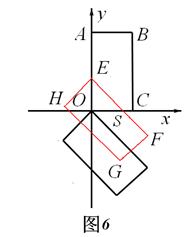
∴(Ⅰ)当0<t≤2时,矩形EFHG与矩形OABC重叠部分的面积为△OCS的面积(如图6).此时,OE="OS=" t, ∴
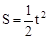 .
.
(Ⅱ)当2<t≤
 时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.
时,矩形EFHG与矩形OABC重叠部分的面积为直角梯形OEPC的面积(如图7).此时OE= t,,OC=2.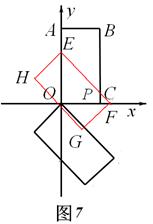
由E(0,t),∠FFO=450,用用待定系数法求得直线EP的解析式为
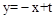 .
.当x=2时,
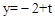 . ∴CP=
. ∴CP=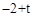 . ∴
. ∴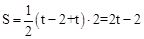 .
.(Ⅲ)当
 <t≤
<t≤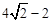 时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),
时,矩形EFHG与矩形OABC重叠部分的面积为五边形EQCUV的面积(如图8),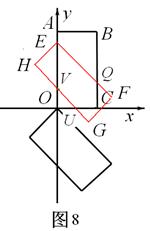
它等于直角梯形EQCO的面积减去直角三角形VOU的的面积.
此时,OE= t,,OC=2,CQ=
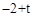 ,OU="OV=" t-
,OU="OV=" t- .
.∴
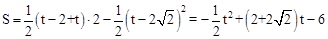 .
.综上所述,当0<t≤
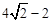 时,S与t之间的函数关系式为
时,S与t之间的函数关系式为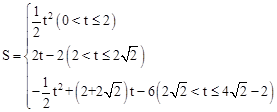 .
.
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 的对称轴是 .
的对称轴是 .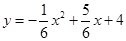 与直线
与直线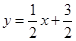 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.

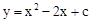 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】 的图象如图所示,则函数
的图象如图所示,则函数 与
与 在同一直角坐标系内的大致图象是( )
在同一直角坐标系内的大致图象是( )

 ,则此二次函数( )
,则此二次函数( ) 向下平移1个单位,得到的抛物线是( ).
向下平移1个单位,得到的抛物线是( ).



 、二次函数
、二次函数 和反比例函数
和反比例函数 在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】
在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】



