题目内容
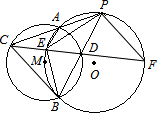 如图,M为⊙O上的一点,⊙M与⊙O相交于A、B两点,P为⊙O上任意一点,直线PA、PB分别交⊙M于C、D两点,直线CD交⊙O于E、F两点,连接PE、PF、BC,下列结论,其中正确的有
如图,M为⊙O上的一点,⊙M与⊙O相交于A、B两点,P为⊙O上任意一点,直线PA、PB分别交⊙M于C、D两点,直线CD交⊙O于E、F两点,连接PE、PF、BC,下列结论,其中正确的有
①PE=PF;②PE2=PA•PC;③EA•EB=EC•ED;④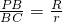 (其中R、r分别为⊙O、⊙M的半径)
(其中R、r分别为⊙O、⊙M的半径)
- A.①②③
- B.①②④
- C.②④
- D.①②③④
D
分析:首先利用圆周角定理以及三角形的外角证明∠F=∠PEF,即可得出PE=PF,再利用圆周角定理证明△PAE∽△PEC,得出PE2=PA•PC,作直径CH,PN,得出△BCH∽△BPN,
即可得出 =
=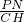 =
=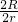 =
=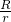 ,最后证明PC=PB,得出
,最后证明PC=PB,得出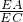 =
=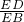 ,即EA•EB=EC•ED.
,即EA•EB=EC•ED.
解答: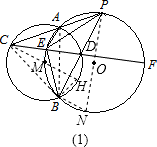 解:连接AB,
解:连接AB,
∵ =
= ,
,
∴∠APE=∠ABE,
∵∠PEF=∠ACD+∠APE,
=∠ABP+∠ABE,
=∠PBE,
∵ =
= ,
,
∴∠F=∠PBE,
∴∠F=∠PEF,
∴PE=PF,故①选项正确;
∵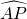 =
=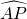 ,
,
∴∠ABP=∠AEP,
∵ =
= ,
,
∴∠ABP=∠ACD,
∴∠AEP=∠ACD,
∵∠APE=∠APE,
∴△PAE∽△PEC,
∴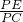 =
= ,
,
∴PE2=PA•PC,故②正确;
作直径CH,连接BH,∴∠CBH=90°,
作直径PN,连接BN,∴∠PBN=90°,
∴∠CBH=∠PBN,
∵ =
= ,
,
∴∠BAC=∠H,
∵∠BAC=∠N(圆内接四边形的外角等于内对角),
∴∠H=∠N,
△BCH∽△BPN,
∴ =
=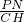 =
=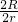 =
=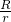 ,故此④选项正确;
,故此④选项正确;
如图(2)连接MA,MB,MC,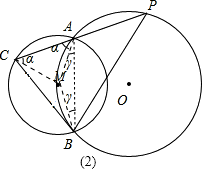
∴MA=MB=MC,
设∠MAC=∠MCA=α,
∠MCB=∠MBC=β,
∠MAB=∠MBA=γ,
∵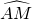 =
=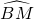 =
=
 ,
,
∴∠MAB=∠MBA= ∠APB,
∠APB,
∴∠APB=2γ,
∴∠CAB=∠APB+∠ABP,
α+γ=2γ+∠ABP,
∴∠ABP=α-γ,
∴∠PBC=∠ABP+∠ABC=α-γ+β+γ=α+β,
∴∠PCB=α+β,∴∠PBC=∠PCB,
∴PC=PB,
如图(1)∵PE=PF,PE2=PA•PC=PD•PB,
∴PE•PF=PD•PC,
∴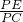 =
=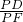 ,
,
∵△PAE∽△PEC,
∴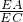 =
=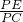 ,
,
∵△BDE∽△FDP,
∴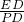 =
=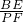 ,
,
∴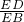 =
=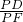 ,
,
∴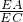 =
=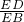 ,
,
∴EA•EB=EC•ED,
∴③选项正确,
故①②③④都正确,
故选:D.
点评:此题主要考查了相似三角形的判定与性质以及圆周角定理和圆内有关性质等知识,根据已知的作出连接两圆交点的辅助线利用三角形相似得出是解题关键,此题难度较大.
分析:首先利用圆周角定理以及三角形的外角证明∠F=∠PEF,即可得出PE=PF,再利用圆周角定理证明△PAE∽△PEC,得出PE2=PA•PC,作直径CH,PN,得出△BCH∽△BPN,
即可得出
 =
=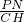 =
=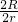 =
=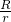 ,最后证明PC=PB,得出
,最后证明PC=PB,得出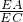 =
=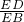 ,即EA•EB=EC•ED.
,即EA•EB=EC•ED.解答:
 解:连接AB,
解:连接AB,∵
 =
= ,
,∴∠APE=∠ABE,
∵∠PEF=∠ACD+∠APE,
=∠ABP+∠ABE,
=∠PBE,
∵
 =
= ,
,∴∠F=∠PBE,
∴∠F=∠PEF,
∴PE=PF,故①选项正确;
∵
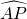 =
=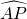 ,
,∴∠ABP=∠AEP,
∵
 =
= ,
,∴∠ABP=∠ACD,
∴∠AEP=∠ACD,
∵∠APE=∠APE,
∴△PAE∽△PEC,
∴
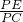 =
= ,
,∴PE2=PA•PC,故②正确;
作直径CH,连接BH,∴∠CBH=90°,
作直径PN,连接BN,∴∠PBN=90°,
∴∠CBH=∠PBN,
∵
 =
= ,
,∴∠BAC=∠H,
∵∠BAC=∠N(圆内接四边形的外角等于内对角),
∴∠H=∠N,
△BCH∽△BPN,
∴
 =
=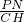 =
=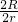 =
=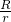 ,故此④选项正确;
,故此④选项正确;如图(2)连接MA,MB,MC,

∴MA=MB=MC,
设∠MAC=∠MCA=α,
∠MCB=∠MBC=β,
∠MAB=∠MBA=γ,
∵
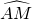 =
=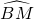 =
=
 ,
,∴∠MAB=∠MBA=
 ∠APB,
∠APB,∴∠APB=2γ,
∴∠CAB=∠APB+∠ABP,
α+γ=2γ+∠ABP,
∴∠ABP=α-γ,
∴∠PBC=∠ABP+∠ABC=α-γ+β+γ=α+β,
∴∠PCB=α+β,∴∠PBC=∠PCB,
∴PC=PB,
如图(1)∵PE=PF,PE2=PA•PC=PD•PB,
∴PE•PF=PD•PC,
∴
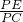 =
=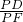 ,
,∵△PAE∽△PEC,
∴
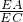 =
=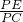 ,
,∵△BDE∽△FDP,
∴
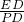 =
=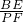 ,
,∴
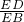 =
=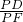 ,
,∴
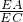 =
=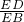 ,
,∴EA•EB=EC•ED,
∴③选项正确,
故①②③④都正确,
故选:D.
点评:此题主要考查了相似三角形的判定与性质以及圆周角定理和圆内有关性质等知识,根据已知的作出连接两圆交点的辅助线利用三角形相似得出是解题关键,此题难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
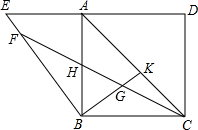 如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK于点G.
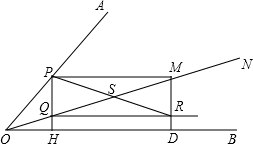
如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK于点G.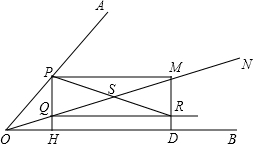 如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S. 如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK于点G.
如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK于点G.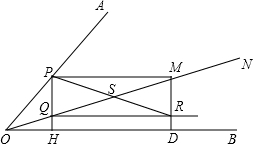 如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.