题目内容
如图1,在Rt△ABC中,∠C=90°,BC=8厘米,AC=12厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒是k厘米;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求k的值和y2与x的函数关系;
(3)在图2中,设y1与y2的图象的交点为M,点G是x轴正半轴上一点(0<OG<6),过G作EF垂直于x轴,分别与y1、y2的
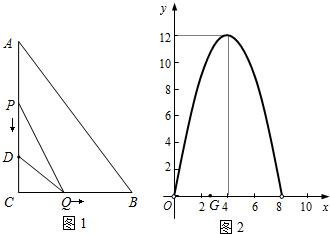 图象交于点E、F.求△OMF面积的最大值.
图象交于点E、F.求△OMF面积的最大值.①说出线段EF的长在图1中所表示的实际意义;
②求△OMF面积的最大值.
分析:(1)直接根据三角形的面积公式可得y1=
x;
(2)先设y2=
x(12-kx)=-
x2+6x,把x=12时,y2=12代入解析式可求得k=
,即y2=-
x2+6x;
(3)①线段是长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ的面积),由
x=-
x2+6x得点M(6,9),过点M做MH⊥EF于点H,则S△OMF=S△OEF+S△MEF=3EF=3(-
x2+6x-
x)=-
(x-3)2+
,所以当x=3时,△OMF的面积有最大值为
.
| 3 |
| 2 |
(2)先设y2=
| 1 |
| 2 |
| k |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
(3)①线段是长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ的面积),由
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 81 |
| 4 |
| 81 |
| 4 |
解答: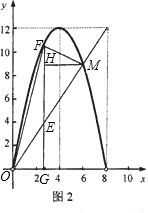 解:(1)y1=
解:(1)y1=
x
画图正确(2分)
(2)y2=
x(12-kx)=-
x2+6x (4分)
由题设:当x=4时,y2=12,
所以-8k+24=12,
解得k=
(5分)
从而y2=-
x2+6x (6分)
(3)①线段是长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ的面积)(7分)
②解法一:由
x=-
x2+6x
得点M(6,9)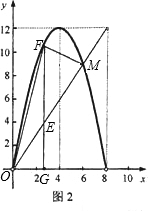
过点M做MH⊥EF于点H,则S△OMF=S△OEF+S△MEF=
EF.
OG+
EF.MH=
EF×6=3EF(9分)
=3(-
x2+6x-
x)=-
(x-3)2+
(10分)
所以当x=3时,△OMF的面积有最大值为
(12分)
解法二:由
x=-
x2+6x得点M(6,9)
过点M做MH⊥x轴于点N,则
S△OMF=S四边形ONMF-S△ONM=S△OGF+S梯形FGNM-S△ONM(9分)
=-
x2+
x (10分)
所以当x=3时,△OMF的面积有最大值为
.(12分)
 解:(1)y1=
解:(1)y1=| 3 |
| 2 |
画图正确(2分)
(2)y2=
| 1 |
| 2 |
| k |
| 2 |
由题设:当x=4时,y2=12,
所以-8k+24=12,
解得k=
| 3 |
| 2 |
从而y2=-
| 3 |
| 4 |
(3)①线段是长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ的面积)(7分)
②解法一:由
| 3 |
| 2 |
| 3 |
| 4 |
得点M(6,9)

过点M做MH⊥EF于点H,则S△OMF=S△OEF+S△MEF=
| 1 |
| 2 |
OG+
| 1 |
| 2 |
| 1 |
| 2 |
=3(-
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 81 |
| 4 |
所以当x=3时,△OMF的面积有最大值为
| 81 |
| 4 |
解法二:由
| 3 |
| 2 |
| 3 |
| 4 |
过点M做MH⊥x轴于点N,则
S△OMF=S四边形ONMF-S△ONM=S△OGF+S梯形FGNM-S△ONM(9分)
=-
| 9 |
| 4 |
| 27 |
| 2 |
所以当x=3时,△OMF的面积有最大值为
| 81 |
| 4 |
点评:本题结合三角形的性质考查二次函数的综合应用,函数和几何图形的综合题目,要利用三角形的性质和二次函数的性质把数与形有机的结合在一起,利用图形间的“和差“关系求解.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目