题目内容
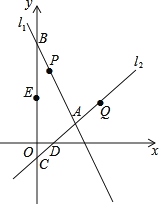
【题目】已知：如图，直线y1＝x+1在平面直角坐标系xOy中．
（1）在平面直角坐标系xOy中画出y2＝﹣2x+4的图象；
（2）求y1与y2的交点坐标；
（3）根据图象直接写出当y1≥y2时，x的取值范围．
【答案】（1）y2＝﹣2x+4的图象如图所示，见解析；（2）y1与y2的交点坐标为（1，2）；（3）x的取值范围是x≥1．
【解析】
（1）依据函数解析式即可画出y2=-2x+4的图象；
（2）解方程组可得y1与y2的交点坐标；
（3）依据函数图象以及交点坐标即可得到当y1≥y2时，x的取值范围．
（1）y2＝﹣2x+4的图象如图所示：
（2）解方程组
，可得
，
∴y1与y2的交点坐标为（1，2）；
（3）当y1≥y2时，x的取值范围是x≥1．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
【题目】某天上午7：30，小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8：30的动车．记汽车的行驶时间为t小时，行驶速度为v千米/小时（汽车行驶速度不超过60千米/小时）．根据经验，v，t的一组对应值如下表：
V（千米/小时） | 20 | 30 | 40 | 50 | 60 |
T（小时） | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
（1）根据表中的数据描点，求出平均速度v（千米/小时）关于行驶时间t（小时）的函数表达式；
（2）若小芳从开始打车到上车用了10分钟，小芳想在动车出发前半小时到达动车站，若汽车的平均速度为32千米/小时，小芳能否在预定的时间内到达动车站？请说明理由；
（3）若汽车到达动车站的行驶时间t满足0.3＜t＜0.5，求平均速度v的取值范围．
