题目内容
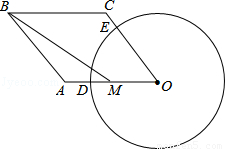
已知四边形OABC是边长为4的正方形,分别以OA、OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A、C两点.
(1)求直线l的函数表达式;
(2)若P是直线l上的一个动点,请直接写出当△OPA是等腰三角形时点P的坐标;
(3)如图2,若点D是OC的中点,E是直线l上的 一个动点,求使OE+DE取得最小值时点E的坐标.
一个动点,求使OE+DE取得最小值时点E的坐标.
(1)求直线l的函数表达式;
(2)若P是直线l上的一个动点,请直接写出当△OPA是等腰三角形时点P的坐标;
(3)如图2,若点D是OC的中点,E是直线l上的
 一个动点,求使OE+DE取得最小值时点E的坐标.
一个动点,求使OE+DE取得最小值时点E的坐标.分析:(1)易得A,C两点的坐标,设出一次函数解析式,把这两点代入可得所求函数解析式;
(2)分别以点O或点A为圆心,以OA长为半径画弧,可得3个可能的点P,作出OA的垂直平分线可得第4个点P;
(3)易得点O与点B关于直线l对称,那么连接BD,与l的交点即为点E,得到DB的解析式与l的解析式联立可得E的坐标.
(2)分别以点O或点A为圆心,以OA长为半径画弧,可得3个可能的点P,作出OA的垂直平分线可得第4个点P;
(3)易得点O与点B关于直线l对称,那么连接BD,与l的交点即为点E,得到DB的解析式与l的解析式联立可得E的坐标.
解答:解:(1)设直线l的函数表达式y=kx+b(k≠0),经过A(4,0)和C(0,4)得
,
解之得
,
∴直线l的函数表达式y=-x+4;
(2)P1(0,4)、P2(2,2)、P3 (4-2
,2
)、P4(4+2
,-2
);
(3)∵O与B关于直线l对称,
∴连接DB,交AC于点E,则点E为所求,此时OE+DE取得最小值,
 设DB所在直线为y=k1x+b1 (k1≠0),经过点D(0,2)、B(4,4)
设DB所在直线为y=k1x+b1 (k1≠0),经过点D(0,2)、B(4,4)
,
解得
∴直线DB为y=
x+2,
解方程组:
,得
,
∴点E的坐标为(
,
).
|
解之得
|
∴直线l的函数表达式y=-x+4;
(2)P1(0,4)、P2(2,2)、P3 (4-2
| 2 |
| 2 |
| 2 |
| 2 |
(3)∵O与B关于直线l对称,
∴连接DB,交AC于点E,则点E为所求,此时OE+DE取得最小值,
 设DB所在直线为y=k1x+b1 (k1≠0),经过点D(0,2)、B(4,4)
设DB所在直线为y=k1x+b1 (k1≠0),经过点D(0,2)、B(4,4)
|
解得
|
∴直线DB为y=
| 1 |
| 2 |
解方程组:
|
|
∴点E的坐标为(
| 4 |
| 3 |
| 8 |
| 3 |
点评:考查一次函数的应用;在本题中应注意可能为等腰三角形的不同情况;在求平面图形中的最短距离和时,应找到特殊点关于直线的对应点.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数
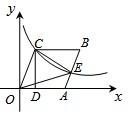
如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数 (2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
(2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
 如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=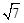 ,
,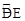 的长是
的长是 .求证:直线BC与⊙O相切.
.求证:直线BC与⊙O相切.