题目内容
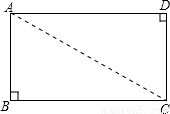
 如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,点B恰好落在AC上,则AC的长是________.
如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC,若将纸片沿AE折叠,点B恰好落在AC上,则AC的长是________.
4
分析:根据折叠的性质及等边对等角的性质,可得到∠BAE=∠EAC=∠ECA,根据三角形内角和定理即可求得∠ECA的度数,再根据直角三角形的性质不难求得AC的长.
解答:∵AE=EC
∴∠EAC=∠ECA
∵将纸片沿AE折叠,点B恰好落在AC上
∴∠BAE=∠EAC
∴∠BAE=∠EAC=∠ECA
∵∠B+∠ECA+∠CAB=180°
∴∠ECA=30°
∵AB=2
∴AC=2AB=4.
故填4.
点评:本题考查等腰三角形的性质及直角三角形性质和翻折变换等知识;对于翻折变换问题,找准对应的相等关系是正确解答的关键.
分析:根据折叠的性质及等边对等角的性质,可得到∠BAE=∠EAC=∠ECA,根据三角形内角和定理即可求得∠ECA的度数,再根据直角三角形的性质不难求得AC的长.
解答:∵AE=EC
∴∠EAC=∠ECA
∵将纸片沿AE折叠,点B恰好落在AC上
∴∠BAE=∠EAC
∴∠BAE=∠EAC=∠ECA
∵∠B+∠ECA+∠CAB=180°
∴∠ECA=30°
∵AB=2
∴AC=2AB=4.
故填4.
点评:本题考查等腰三角形的性质及直角三角形性质和翻折变换等知识;对于翻折变换问题,找准对应的相等关系是正确解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
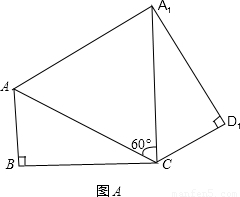
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
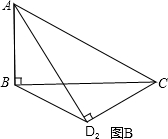

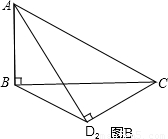
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
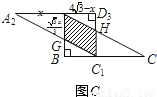
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



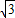 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: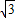 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.