题目内容
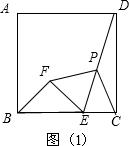
如图，正方形ABCD中，E是CD的中点，AE的垂直平分线FM交AB的延长线于F，交BC于P，连接EF，交BC于G，求EP：PC的值．
设正方形ABCD的边长是2x，则AD=AB=CD=BC=2x，
∵E是CD的中点，
∴DE=CE=x，
∵正方形ABCD，
∴∠D=∠ABC=90°，
由勾股定理得：AE=
=
x，
∵AB∥CD，
∴∠FAE=∠DEA，
∵AE的垂直平分线FM，
∴AM=ME=
AE=
x，∠AMF=∠D=90°，
∴△FMA∽△ADE，
∴
=
，
∴AF=
x，
由勾股定理得：FM=
=
x，
∴BF=AF-AB=
x，
∵正方形ABCD，AE的垂直平分线FM，
∴∠FBP=∠FMA=90°，
∵∠PFB=∠AFM，
∴△PFB∽△AFM，
∴
=
，
∴BP=
x，
∴CP=2x-
x=
x，
由勾股定理得：EP=
=
x，
∴EP：PC的值是
．
答：EP：PC的值是
．
∵E是CD的中点，
∴DE=CE=x，
∵正方形ABCD，
∴∠D=∠ABC=90°，
由勾股定理得：AE=
| AD2+DE2 |
| 5 |
∵AB∥CD，
∴∠FAE=∠DEA，
∵AE的垂直平分线FM，
∴AM=ME=
| 1 |
| 2 |
| ||
| 2 |
∴△FMA∽△ADE，
∴
| AF |
| AE |
| AM |
| DE |
∴AF=
| 5 |
| 2 |
由勾股定理得：FM=
| AF2-AM2 |
| 5 |
∴BF=AF-AB=
| 1 |
| 2 |
∵正方形ABCD，AE的垂直平分线FM，
∴∠FBP=∠FMA=90°，
∵∠PFB=∠AFM，
∴△PFB∽△AFM，
∴
| BP |
| AM |
| BF |
| FM |
∴BP=
| 1 |
| 4 |
∴CP=2x-
| 1 |
| 4 |
| 7 |
| 4 |
由勾股定理得：EP=
| CP2+CE2 |
| ||
| 4 |
∴EP：PC的值是
| ||
| 7 |
答：EP：PC的值是
| ||
| 7 |
练习册系列答案
相关题目
