题目内容
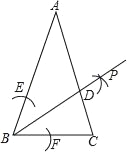
【题目】已知：如图，点E、F分别是AB、CD上的点，DE、AF分别交BC于G、H，∠A=∠D，∠1=∠2，试说明∠B=∠C．阅读下面的解题过程，在横线上补全推理过程或依据．
解：∵∠1=∠2（已知）
∠1=∠3（______________________________）
∴∠2=∠3（等量代换）
∴AF∥DE（_____________________________）
∴∠4=∠D（__________________________________）
又∵∠A=∠D （已知）
∴∠4=∠A（等量代换）
______（____________________________________）
∴∠B=∠C （_________________________________）
【答案】对顶角相等 同位角相等，两直线平行 两直线平行，同位角相等 AB∥CD 内错角相等，两直线平行 两直线平行，内错角相等
【解析】
本题主要考查平行线的判定以及性质，根据内错角相等，同位角相等即可判定平行，反之推角等．
由图示可知∠1，∠3关系为对顶角，对顶角性质为相等，故答题空1应填对顶角相等作为依据；
因为∠2，∠3关系为同位角且相等，由其推出平行，故答题空2依据是同位角相等，两直线平行；
因为∠D，∠4关系为同位角，且由AF∥DE推出其相等，故答题空3依据是两直线平行，同位角相等；
因为∠4，∠A关系为内错角且相等，故可推出答题空4为AB∥CD，答题空5依据是内错角相等，两直线平行；
因为∠B，∠C关系为内错角，且由AB∥CD推出其相等，故答题空6依据为两直线平行，内错角相等．
【题目】为了进一步了解七年级800名学生的身体素质情况，体育老师抽取七年级男女各25位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图．如下所示：
组别 | 次数x | 频数（人数） |
第1组 | 80≤x＜100 | 6 |
第2组 | 100≤x＜120 | 8 |
第3组 | 120≤x＜140 |
|
第4组 | 140≤x＜160 | 16 |
第5组 | 160≤x＜180 | 6 |
请结合图表完成下列问题：
(1)表中的
，跳绳次数低于140次的有
人，则
(2)请把频数分布直方图补充完整；
（3）若七年级学生一分钟跳绳次数（x）达标要求是：x≥120．请估算七年级学生达标人数．
【题目】某公司计划开发
、
两种户型楼盘，设户型
套，户型
套，且两种户型的函数关系满足
，经市场调研，每套户型的成本价和预售价如下表所示：
楼盘户型 |
|
|
成本价（万元/套） | 60 | 80 |
预售价（万元/套） | 80 | 120 |
若公司最多投入开发资金为14000万元，所获利润为
万元，
（1）求与的函效关系式和自变量的取值范围
（2）售完这批楼盘，公司所获得的最大利润是多少？
（3）公司在实际销售过程中，其他条件不变，户型每套销售价格提高
（
）万元，且限定户型最多开发120套，则公司如何建房，利润最大？（注：利润=售价－成本．）